Operaciones algebraicas con funciones

Si se conocen dos funciones $f(x)$ y $g\;(x)$ con dominios $D_f$ y $D_g$ se pueden construir otras funciones en términos de ellas, como son:

1. La suma: $(f+g\;)(x) = f(x) + g\;(\;x\;)$ cuyo dominio será $D_{f + g}$ = $D_f ∩ D_g$ ya que para poder evaluar la suma lo único que se requiere es poder evaluar los dos sumandos; por eso es intersección, los elementos en el dominio de la suma deben pertenecer al dominio de $f(x)$ y también al dominio de $g\;(x)$.
   
   Se recuerda que el dominio de una función es el conjunto de valores donde se puede evaluar la función.


2. La resta: $(f–g\;)(x) = f(x) – g\;(x)$ cuyo dominio será $D_{f - g} = D_f ∩ D_g$ ya que para poder evaluar la resta lo único que se requiere es poder evaluar los dos términos que se van a restar.


3. El producto: $(f g\;)(x) = f(x) g\;(x)$ cuyo dominio será $D_{f g} = D_f ∩ D_g$ igual que en los casos anteriores, para poder evaluar un producto, lo único que se requiere es poder evaluar los dos factores.


4. El cociente: $(\frac{f}{g})(x) = \frac{f(x)}{g\;(x)}$ cuyo dominio será $D_{\frac{f}{g}} = D_ f ∩ D_g$ menos los valores donde $g\;(x)=0$; para poder evaluar el cociente se debe poder evaluar el numerador y el denominador y además el denominador debe ser diferente de cero.


5. La composición: $(f ∘ g)(x) = f (\;g\;(x))$ que se lee "$f$ bolita $g$" y cuyo dominio es $D_{f ∘ g} = D_g ∩ (g\;(x) ∈ D_f )$ porque para poder evaluar la composición se debe poder evaluar $g\;(x)$ que entra como el argumento de $f$ y ese valor de $g\;(x)$ debe pertenecer al dominio de $f$ .

Por ejemplo:

Si $f(x)=\frac{2}{(x^2-9)}$ y $g\;(x)=\sqrt{x^2-4 }$

1. Obtener $(f ∘ g\;)(x)$ y su dominio,


2. Obtener $(\frac{g}{f})(x)$ y su dominio.

Solución:

1. $(f ∘ g\;)(x) = f (g\;(x)) = f (\sqrt{x^2-4}) = \frac{2}{{(\sqrt{x^2-4} )}^2-9}=\frac{2}{x^2-4 -9}=\frac{2}{x^2-13}$.
   
   El dominio se puede calcular mediante la fórmula o de la expresión que es más sencillo, pero tomando en cuenta las simplificaciones efectuadas, en este caso: $(\sqrt{x^2-4})^2=x^2-4$ sólo si $x^2-4 ≥ 0$
   
   Si no es así se sale de los reales; entonces es la primera condición que se debe tomar en cuenta; su solución es $x ∈(-\infty ,- 2]∪ [2 ,\infty)$ .
   
   Y la segunda condición es que: $x^2-13 ≠ 0$ , esto es $x ≠ ±\sqrt{13}≈ ±3.61$.
   
   Intersectando los dos resultados:
   
   

      

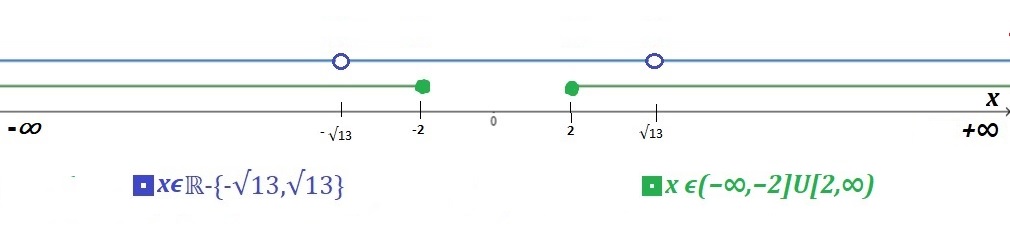
   ya que deben cumplirse ambas condiciones, se tiene:
   
   

      

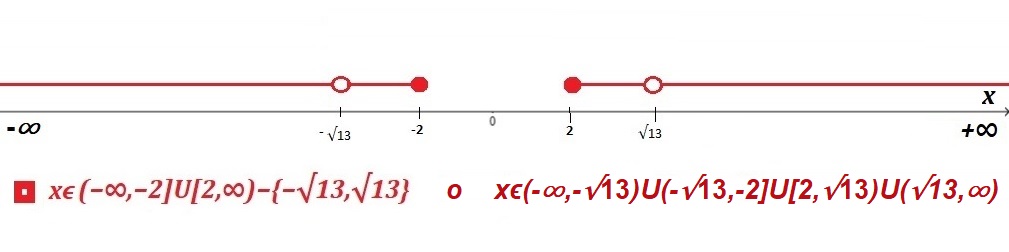
   Así:
   
                     $D_{f ∘ g}=(-\infty ,- 2]∪ [2 ,\infty)-${$-\sqrt{13}, \sqrt{13}$} $$o$$ $$D_{f ∘ g}=(-\infty ,-\sqrt{13})∪ (-\sqrt{13},-2]∪ [2,\sqrt{13})∪ (\sqrt{13},\infty)$$ .
   
   Aplicando la fórmula quedaría:
   
   $D_{f ∘ g}=D_g ∩ (g\;(x) ∈ D_f)=$
   
   $=( (-\infty ,- 2]∪ [2, \infty))∩(\sqrt{x^2-4} ∈ D_f )=$
   
   $=( (-\infty ,- 2]∪ [2 ,\infty))∩(\sqrt{x^2-4}≠ ± 3)=$
   
   $=( (-\infty ,- 2]∪ [2 ,\infty))∩(x^2-4≠ 9)=$
   
   $=( (-\infty ,- 2]∪ [2 ,\infty))∩(x^2 ≠ 13)=$
   
   $=(-\infty ,- 2]∪ [2 ,\infty)-${$-\sqrt{13}, \sqrt{13}$} Que es el mismo resultado anterior.
   
   
2. $(\frac{g}{f})(x)=\frac{g\;(x)}{f(x)}=\frac{\sqrt{x^2-4}}{\frac{2}{x^2-9}}=\frac{\sqrt{x^2-4}\;(x^2-9)}{2}$
   El dominio se obtendrá de la expresión tomando en cuenta las simplificaciones.
   
   Para que $x^2-9$ suba al numerador, debe ser diferente de cero.
   
   $x^2-9 ≠ 0$, esto es: $x≠ ±3$, primera condición.
   
   Y el contenido del radical debe ser mayor que cero: $x^2-4 ≥ 0$ esto es;
   
   $x ∈(-\infty ,- 2]∪ [2 ,\infty)$, segunda condición.
   
   Para obtener el dominio se intersectan las dos condiciones:
   
   

      

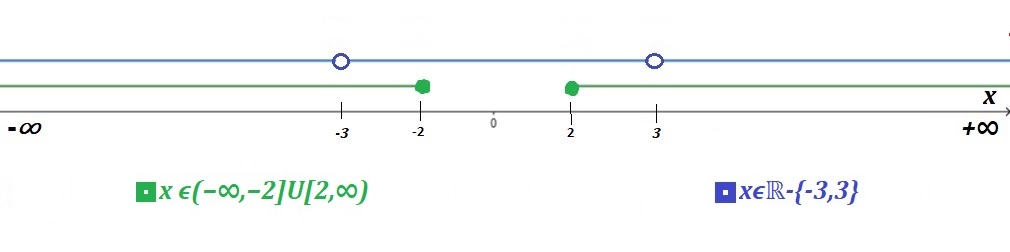
   Así:
   
   

      

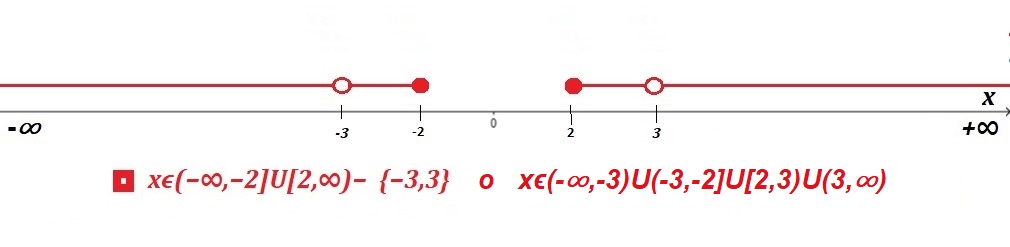
                                 $D_{\frac{g}{f}}=(-\infty ,- 2] ∪ [2 ,\infty)-$ {$-3, 3$} $$o$$ $$D_{\frac{g}{f}}=(-\infty ,- 3) ∪ (-3,-2]∪ [2,3)∪(3,\infty)$$ Que claramente se ve que es la intersección del dominio de $g$ con el de $f$ tomando en cuenta que $f$ nunca vale cero.