


La monotonía de una función se refiere a su crecimiento o decrecimiento.
Se dice que $\boldsymbol{f(x)}$ es creciente en un intervalo $J$
si para toda $ x_2 > x_1 \in J$ se cumple que $f(x_2) > f(x_1)$.
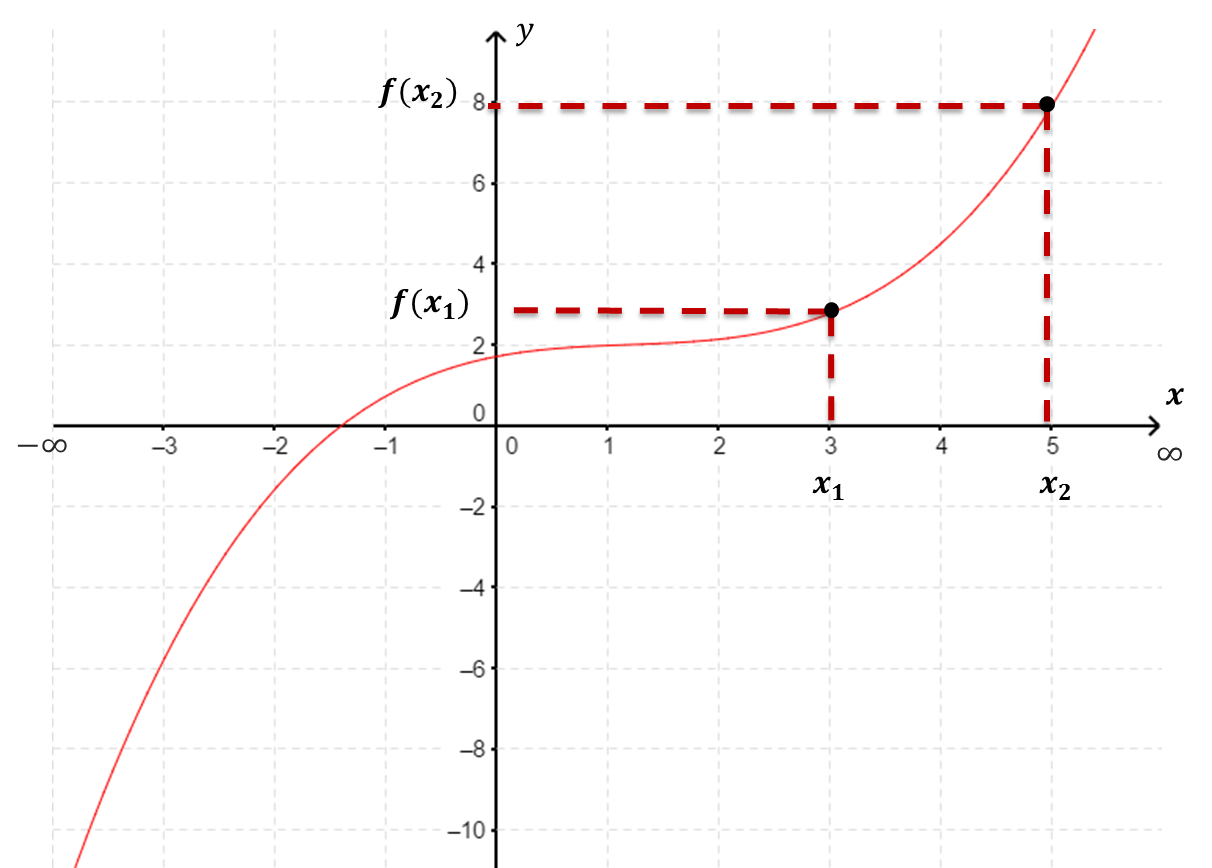 |
|---|
| Función Creciente. |
Gráficamente, la curva sube en el intervalo $J$ (vista de izquierda a derecha, como lo indica el sentido positivo del eje $x$).
Se dice que $\boldsymbol{f(x)}$ es decreciente en un intervalo $J$
si para toda $ x_2 > x_1 \in J$ se cumple que $f(x_2) < f(x_1)$.
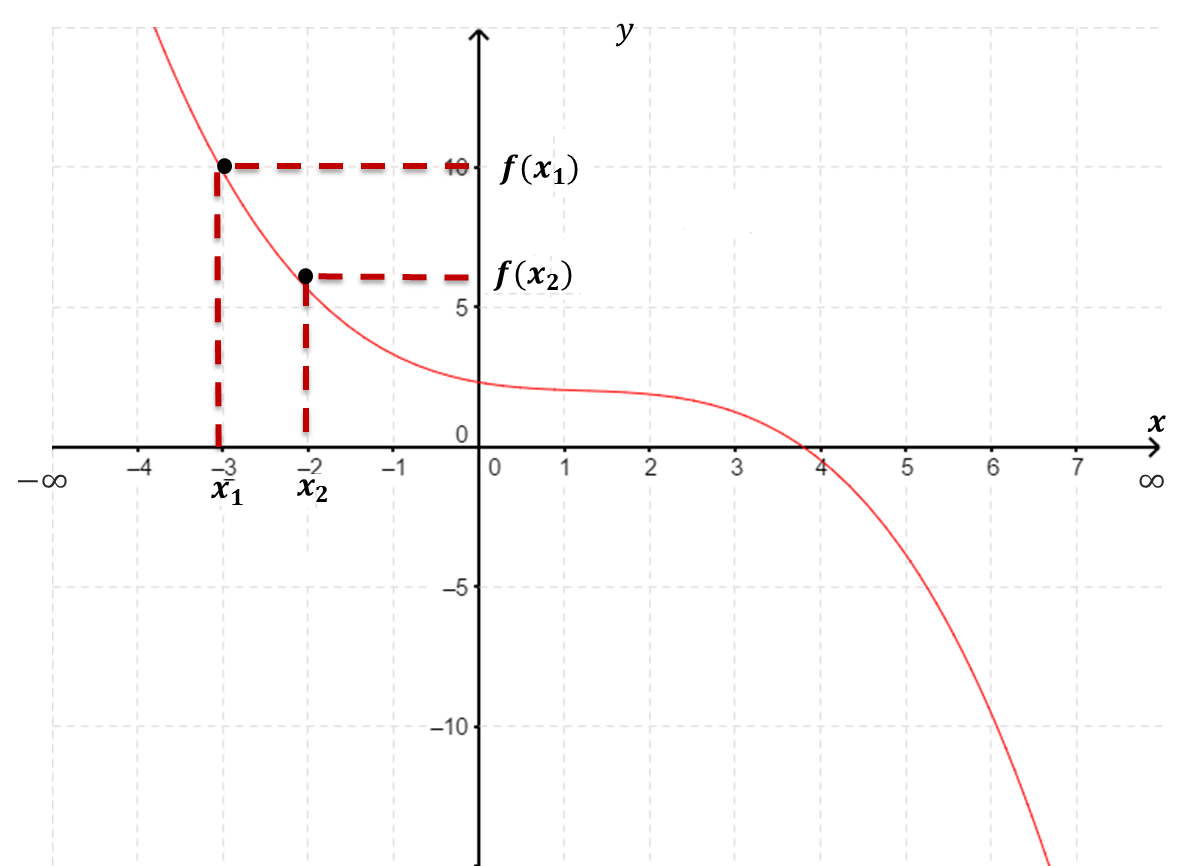 |
|---|
| Función Decreciente. |
Gráficamente, la curva baja en el intervalo $J$ (vista de izquierda a derecha, como lo indica el sentido positivo del eje $x$).
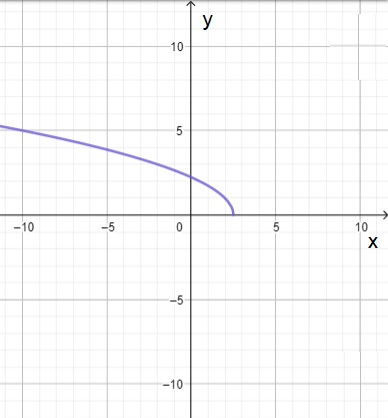
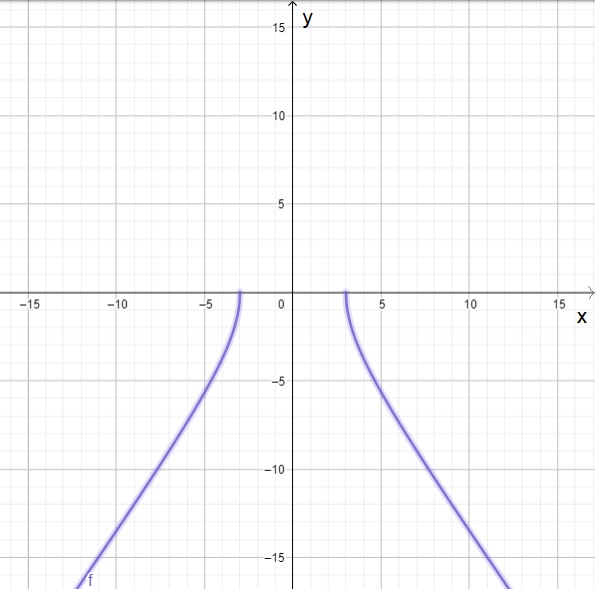
| $f(x)=\sqrt[]{5-2x}$ | $g ( x )$ = $-\sqrt[]{2x^2-18}$ | $j ( x )$ = $\frac{2x}{3x^2-12}$ |
|---|---|---|
 |
 |
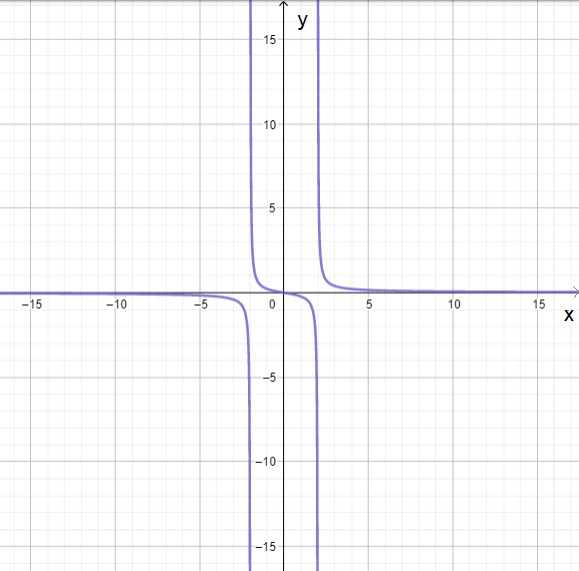 |
| $f(x)$ es decreciente para $x\in(-\infty,\frac{5}{2}]$, $f(x)$ nunca es creciente. | $g(x)$ es creciente para $x\in(-\infty,-3]$, $g(x)$ es decreciente para $x\in[3,\infty)$. | $j(x)$ es decreciente para $x\in(-\infty,-2),$ $(-2,2)$, y $(2,\infty)$. $j(x)$ nunca es creciente. |
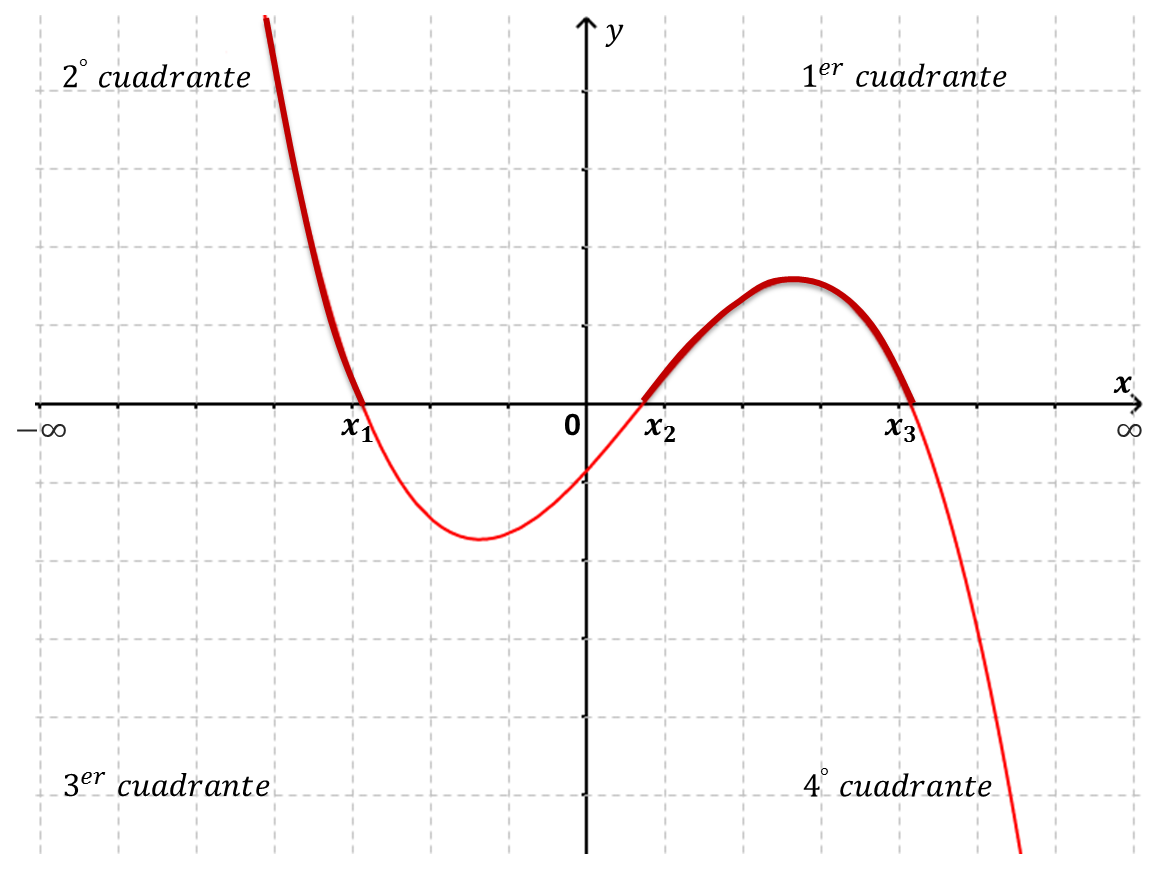
Una función es positiva donde toma valores mayores que cero $\boldsymbol{f(x)>0}$ son los intervalos definidos por los valores de $x$ para los cuales sus imágenes, las $y$ correspondientes, son mayores que cero. Esto es, la resolución de la desigualdad $y=f(x)>0$.
 |
|---|
| $y=f(x)>0$ para $x\in(-\infty ,x_1) \cup (x_2,x_3) $ |
Geométricamente, como los puntos sobre el eje $x$ tienen $y=0$, la porción de la gráfica de $f(x)$, correspondiente a los valores positivos de la función, se encontrará por arriba del eje $x$ (en el 1º y/o 2º cuadrantes del sistema de ejes coordenados) donde la ordenada (valor de $y$ ) de todos los puntos coordenados, es positiva.
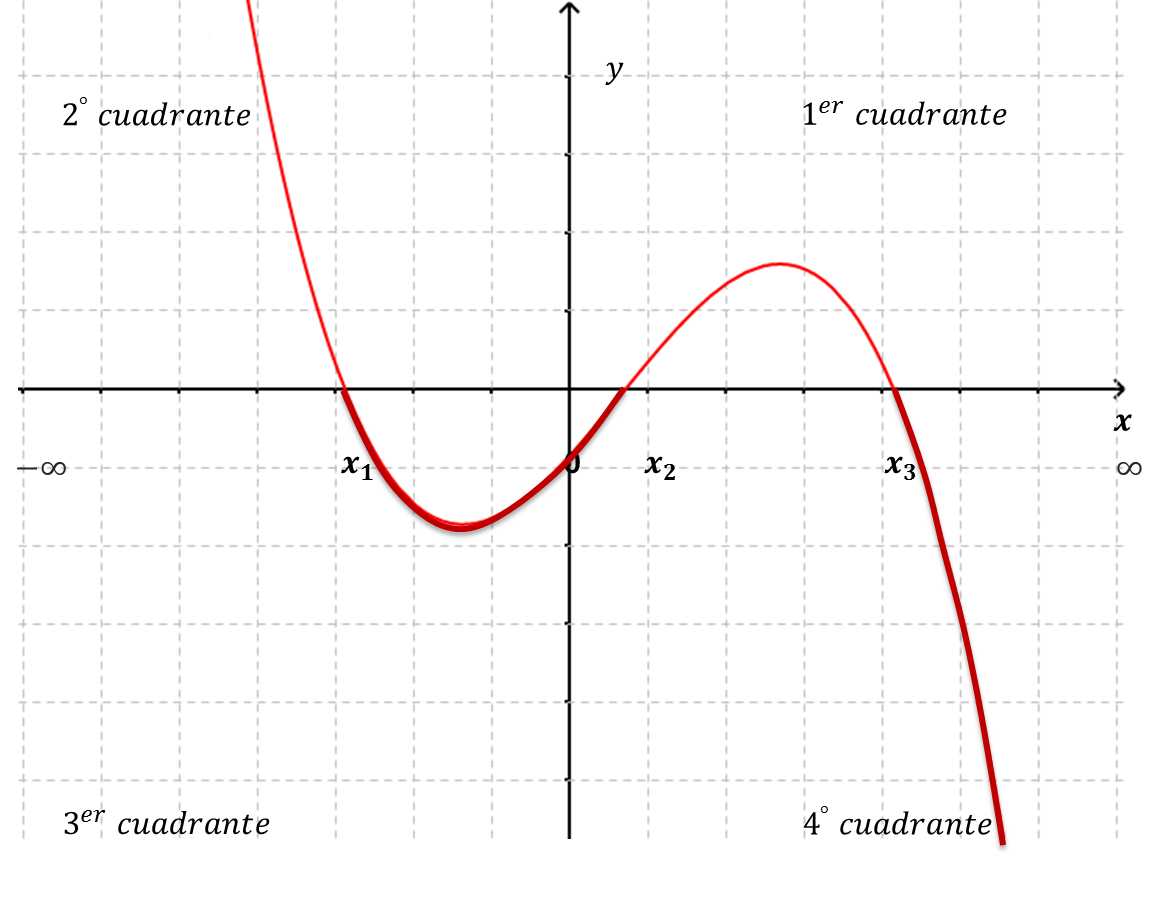
Una función es negativa donde toma valores menores que cero $\boldsymbol{f(x)<0}$ son los intervalos definidos por los valores de $x$ para los cuales sus imágenes, las $y$ correspondientes, son menores que cero. Esto es, la resolución de la desigualdad $y=f(x)<0$ .
 |
|---|
| $y=f(x)<0$ para $x\in(x_1,x_2) \cup (x_3,\infty) $ |
Geométricamente, como los puntos sobre el eje $x$ tienen $y=0$ la porción de la gráfica de $f(x)$, correspondiente a los valores negativos de la función, se encontrará por abajo del eje $x$ (en el 3º y/o 4º cuadrantes del sistema de ejes coordenados) donde la ordenada (valor de $y$) de todos los puntos coordenados, es negativa.
| $f(x)=\sqrt[]{5-2x}$ | $g ( x )$ = $-\sqrt[]{2x^2-18}$ | $j ( x )$ = $\frac{2x}{3x^2-12}$ |
|---|---|---|
 |
 |
 |
| $y=f(x)\geq 0$ para $x\in(-\infty,\frac{5}{2}] $. $y=f(x)\leq 0$ para $x=\frac{5}{2}.$ | $y=g(x)\leq 0$ para $x\in(-\infty,-3] \cup [3,\infty).$ $y=g(x)>0$ para ninguna $x:$ $\boldsymbol\varnothing$. |
$y=j(x)< 0$ para $x\in(-\infty,-2)\cup (0,2) $, $y=j(x)\geq 0$ para $x\in(-2,0]\cup(2,\infty) $ |