


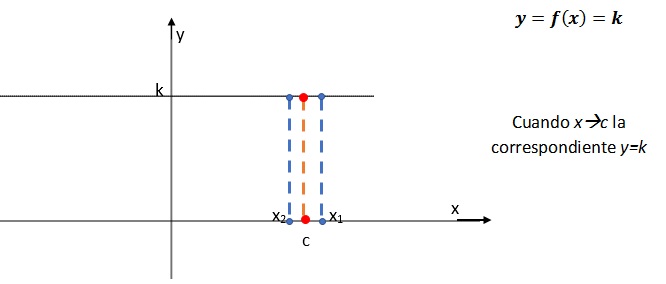
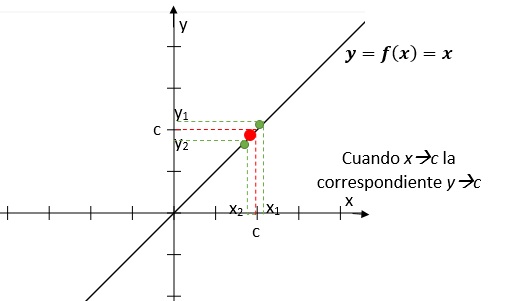
El límite $L$ de una función $y = f ( x )$ cuando $x$ tiende a $c$,
es el valor al que la función (valor de $y$) se acerca o toma,
cuando $x$ se acerca al valor de $c$, sin coincidir nunca con él.
Se denota como:
$$\lim_{x\rightarrow c} f(x)=L$$Se lee: el límite de $f ( x )$ cuando $x$ tiende a $c$ es igual a $L$.
Nótese que:
| $x $ | $y=f (x)$ |
|---|---|
| $x_1 $ | $y_1=f (x_1)$ |
| $x_2 $ | $y_2=f (x_2)$ |
| $x_3 $ | $y_3=f (x_3)$ |
| $...$ |
$...$ |
| $\rightarrow c \;$ con $x≠c $ |
$\rightarrow L \;$ $y_n ≅L$ |
Donde $x_i$ son valores cerca de $c$ (menores y mayores que $c$ ) y $y_i$ son los valores correspondientes de la función en esos puntos.
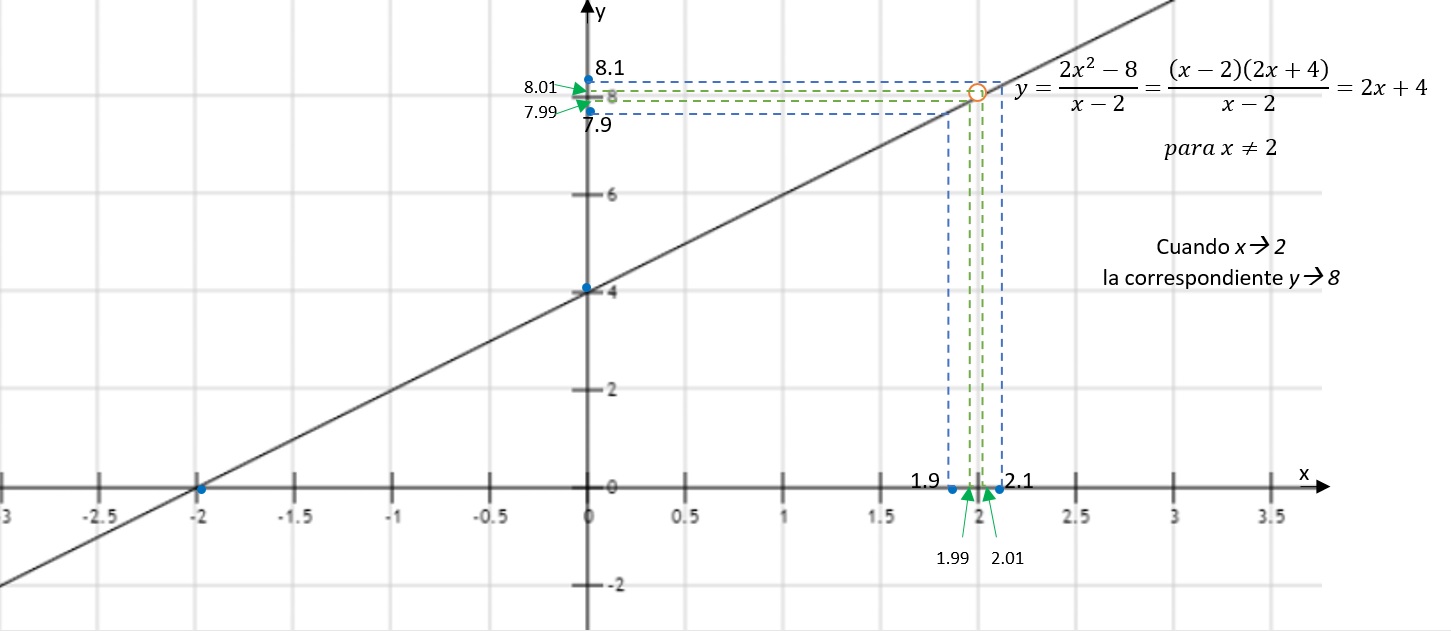
Por ejemplo, calcular $$\lim_{x\rightarrow 2}\frac{2x^2-8}{x-2}\;\; $$
Numéricamente:
| $x $ | $\;\;y=f (x)=\frac {2x^2-8}{x-2}\;\;$ |
|---|---|
| $2.1$ | $y=8.2$ |
| $1.9$ | $y=7.8$ |
| $2.01$ | $y=8.02$ |
| $1.99$ | $y=7.98$ |
| $x_i\rightarrow 2 \;$ con $x≠2 $ |
$y_i≈8$ por lo que se estima que $L=8$ |
Algebraicamente, es mejor, se tiene que: $$\lim_{x\rightarrow 2}\frac{2x^2-8}{x-2}=\lim_{x\rightarrow 2}\frac{2(x-2)(x+2)}{x-2}=\lim_{x\rightarrow 2}2 (x+2)=8\;\;\;\;\; $$
Esto confirma que el límite estimado numéricamente era correcto.
Nótese que se pudo cancelar el factor $x-2$ porque $x ≠ 2$ y entonces ese factor es diferente de cero; además al final se calcula el límite sustituyendo $x = 2$ considerando que es un valor muy cerca de $2$ pero diferente de él.
Gráficamente se puede ver que conforme el valor de $x$ se acerca a $2$ los valores de $y$ se acercan a $8$ aún cuando en $x=2$ no se tiene imagen.
Si en el cálculo del límite de un cociente, queda $\frac{0}{0}\;$ al substituir el valor de $x = c$ se dice que es una forma indeterminada y entonces hay que trabajar algebraicamente la función para remover la indeterminación, como se hizo en el ejemplo anterior.
En general, si se tiene que $$\lim_{x\rightarrow c}f(x)=L$$ $$\lim_{x\rightarrow c}g\;(x)=M$$ entonces:
$$3.-\lim_{x\rightarrow c}(f±g\;)(x)=\lim_{x\rightarrow c}f(x)±\lim_{x\rightarrow c}g\;(x)=L±M\;\;$$ El límite de una suma o resta de dos funciones es la suma o resta de sus límites.
$$4.-\lim_{x\rightarrow c}(f\;g\;)(x)=\lim_{x\rightarrow c}f(x)\lim_{x\rightarrow c}g\;(x)=LM\;\;$$ El límite de un producto de dos funciones es el producto de sus límites.
$$5.-\lim_{x\rightarrow c}(f/g\;)(x)=\lim_{x\rightarrow c}f(x)/\lim_{x\rightarrow c}g\;(x)=\frac{L}{M}\;\;\;$$ El límite de un cociente de dos funciones es el cociente de sus límites, siempre y cuando $\lim_{x\rightarrow c}g(x)≠0$.
Estas tres reglas se pueden justificar tomando en cuenta que cuando $x$ tiende a $c$, $f(x)$ se acerca a $L$ y $g(x)$ se acerca a $M$, intuitivamente se ve que la suma $f+g$ debe acercarse a $L+M$ y entonces el límite de la suma $f+g$ debe ser $L+M$, de manera análoga para la resta, el producto y el cociente cuidando en este último que el denominador sea diferente de cero.
También se tendrá que:
$$6.-\lim_{x\rightarrow c}\sqrt[n] {f (x)}=\;\sqrt[n]{\lim_{x\rightarrow c}f (x)}=\;\sqrt[n] {L} \;\;\;\;\;\; $$ tomando en cuenta que para $n$ par $L$ debe ser mayor que cero.
Si para $n$ par, $L=0$ se debe verificar que cuando $x\rightarrow c\;$, $f(x)$ se acerque a cero tomando únicamente valores positivos para que el resultado esté en los reales, y el límite sea igual a cero. Por ejemplo $\underset{x\to 0}{\lim}\sqrt{x^2}=0\;\;$ pero $\underset{x\to 0}{\lim}\sqrt{x}\;no \;existe\;$ porque cuando $x$ se acerca a cero tomando valores negativos los valores correspondientes de $y=\sqrt{x}\;\;$ no están en los reales.
Nótese que la factorización no debe de ofrecer problema ya que si un polinomio de grado n, $P_n\;(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$, vale cero para un valor de $x$ por ejemplo $x=r$
ese valor es una raíz del polinomio y $x-r$, es un factor en su factorización, esto es: $P_n(x)=(x-r)Q_{n-1}(x)$ donde $Q_{n-1}(x)$ es otro polinomio de grado menor en uno, y $Q_{n-1}(x)=\frac{P_n(x)}{x-r}\;$.
En este caso el polinomio es de $2°$ grado así que conociendo un factor; $(x+2)$ el otro se puede obtener de manera directa.
en este caso el numerador no es un polinomio, por lo que no se tiene un factor, sin embargo se puede racionalizar multiplicando por uno
$$L=\lim_{x\rightarrow -3}\frac{x+\sqrt{2x^2-x-12}}{2x^2+x-15}. \frac{x-\sqrt{2x^2-x-12}}{x-\sqrt{2x^2-x-12}}= $$ $$=\lim_{x\rightarrow -3}\frac{x^2-(2x^2-x-12)}{(2x^2+x-15)(x-\sqrt{2x^2-x-12})}=$$ $$=\lim_{x\rightarrow -3}\frac{-x^2+x+12}{(2x^2+x-15)(x-\sqrt{2x^2-x-12})}:\frac{-9-3+12}{0(-3-3)}=\frac{0}{0}:\;indet\;\;$$ $$L=\lim_{x\rightarrow -3} \frac{(x+3)(-x+4)}{(x+3)(2x-5)(x-\sqrt{2x^2-x-12})}=\lim_{x\rightarrow -3}\frac{-x+4}{(2x-5)(x-\sqrt{2x^2-x-12})}=$$ $$=\frac{3+4}{(-6-5)(-3-3)}=\frac{7}{-11(-6)}=\frac{7}{66}\;\;\;$$