Intervalos de Continuidad y Clasificación de Discontinuidades

Continuidad

Una función es continua en un punto x = c si se satisface que el límite de la función cuando x tiende al valor de c es igual a la imagen en x = c, que es f ( c ), esto es:

Sí $\underset{x\to c}{\lim}f(x)=f(c)$ entonces $f ( x )$ es continua en $x = c$.

Lo que significa que el valor al que la función se acerca o toma, en la vecindad de $x=c$, es el mismo que en el punto $x=c$ por lo que la función es continua en ese punto.

Gráficamente se tiene un trazo continuo de la curva alrededor del punto de coordenadas $(c,f(c))$.

Por ejemplo: ¿$f(x)=\frac{x^2-x-2}{x-2}$ es continua en $x=1$?

Sí porque $\underset{x\to 1}{\lim}f(x)$=$f(1)$.
$\underset{x\to 1}{\lim}\frac{x^2-x-2}{x-2}=\frac{(1)^2-1-2}{1-2}=\frac{-2}{-1}=2$     y     $f(1)=\frac{(1)^2-1-2}{1-2}=\frac{-2}{-1}=2$.

Si analizamos un poco más la función, el dominio es $D_f$=$(-\infty,2)∪(2,\infty)$, $f(2)$ no existe, la función no es continua en $x=2$, pero:

$\underset{x\to 2}{\lim}f(x)=\underset{x\to 2}{\lim}\frac{x^2-x-2}{x-2}=\underset{x\to 2}{\lim}\frac{(x-2)(x+1)}{(x-2)}=\underset{x\to 2}{\lim}\frac{(x+1)}{1}=\frac{(2+1)}{1}=3$,

la función presenta un hueco de coordenadas $(2,3)$.

$y=f(x)=\frac{x^2-x-2}{x-2}$
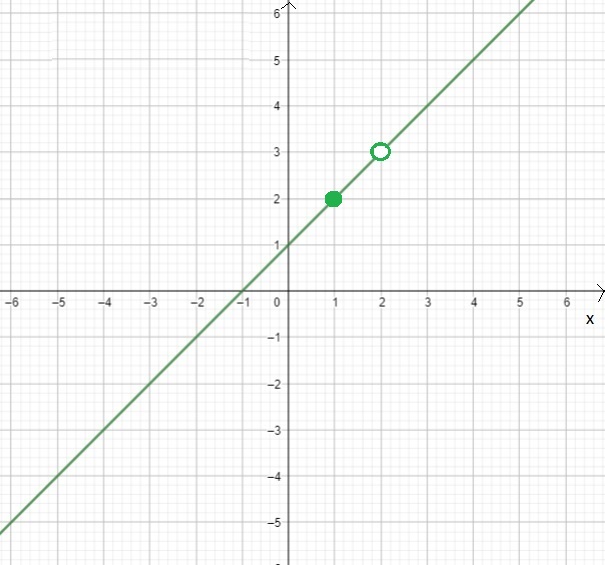$\underset{x\to 2}{\lim}f(x)=3$

Cuando la condición no se cumple se dice que la función es discontinua en ese punto. Esta función es discontinua en $x=2$, $f(2)$ no existe.

La continuidad de una función en un punto se puede extender a todo un intervalo, esto es si:

$\underset{x\to c}{\lim}f(x)=f(c)$ para todo valor de $c∈(a\;,\;b)$ entonces $f ( x )$ es continua en $(\;a\;,\;b\;)$.

Esta función es continua en los intervalos $(-\infty,2)$ y $(2, \infty)$, porque para $c\in D_f$ $\underset{x\to c}{\lim}\frac{x^2-x-2}{x-2}=\frac{c^2-c-2}{c-2}=f(c)$.

Para considerar intervalos cerrados $[a,b]$, además, de comprobar en el intervalo abierto, se debe probar la condición de continuidad en forma lateral en los extremos del intervalo, esto es:

                        $\underset{x\to a^+}{\lim}f(x)=f(a)$       y       $\underset{x\to b^-}{\lim}f(x)=f(b)$

Gráficamente la función no tiene cortes ni agujeros en el intervalo de continuidad.

$Ejemplo$ $1:$ Encontrar el intervalo donde $f(x)=\sqrt[]{9-x^2}$ es continua.

Empezamos por encontrar el dominio: $$9-x^2\geq 0$$ $$x^2\leq 9$$ $$\sqrt[]{x^2}\leq \sqrt[]{9}$$ $$|x|\leq 3$$ $$-3\leq x \leq 3$$ $$D_f = [-3,3]$$ Si $a∈(-3,3)$, $\underset{x\to a}{\lim}\sqrt[]{9-x^2}=\sqrt[]{9-a^2}=f(a)$, $f(x)$ es continua en $x=a$ y por lo tanto en el intervalo $(-3,3)$ y como $\underset{x\to -3^+}{\lim}\sqrt[]{9-x^2}=\sqrt[]{0^+}=0$ y $\underset{x\to 3^-}{\lim}\sqrt[]{9-x^2}=\sqrt[]{0^+}=0$ $f(x)=\sqrt[]{9-x^2}$ es continua en $[-3,3]$.

Clasificación de discontinuidades.

Si $f ( x )$ es discontinua en $x = b$ y se cumple que:

1. Existe $\underset{x\to b}{\lim}f(x)=L$ entonces la discontinuidad es removible y su gráfica presentará un agujero en el punto de coordenadas $( b , L )$.

O bien:


2. No existe $\underset{x\to b}{\lim}f(x)$, o es infinito, entonces la discontinuidad es esencial y su gráfica presentará un salto en $x = b$.

Obtener los intervalos de continuidad y clasificar discontinuidades para:

$$f(x)=\frac{2x^2-3x-2}{x^2+x-6}$$ es continua en su dominio, que es:

$D_f=(-∞ ,-3 )∪(-3 ,2 )∪( 2 ,∞ )$ porque $\underset{x\to a}{\lim}\frac{2x^2-3x-2}{x^2+x-6}= \frac{2a^2-3a-2}{a^2+a-6}$ $=$ $f(a)$ para cualquier valor de $a∈D_f$.


$f(x)$ es discontinua en $x=-3$ y en $x=2$ , su clasificación es la siguiente:

Es discontinua removible en $x=2$ porque $\underset{x\to 2}{\lim}\frac{2x^2-3x-2}{x^2+x-6}$=$\underset{x\to 2}{\lim}\frac{(x-2)(2x+1)}{(x-2)(x+3)}=1$.

Y es discontinua esencial en $x=-3$ porque $\underset{x\to -3}{\lim}\frac{2x^2-3x-2}{x^2+x-6}$ $No$ $existe$, ya que el límite lateral izquierdo $\underset{x\to -3^-}{\lim}\frac{2x^2-3x-2}{x^2+x-6}=∞$ y el límite lateral derecho $\underset{x\to -3^+}{\lim}\frac{2x^2-3x-2}{x^2+x-6}=-∞$ son diferentes.

Su gráfica es:

   

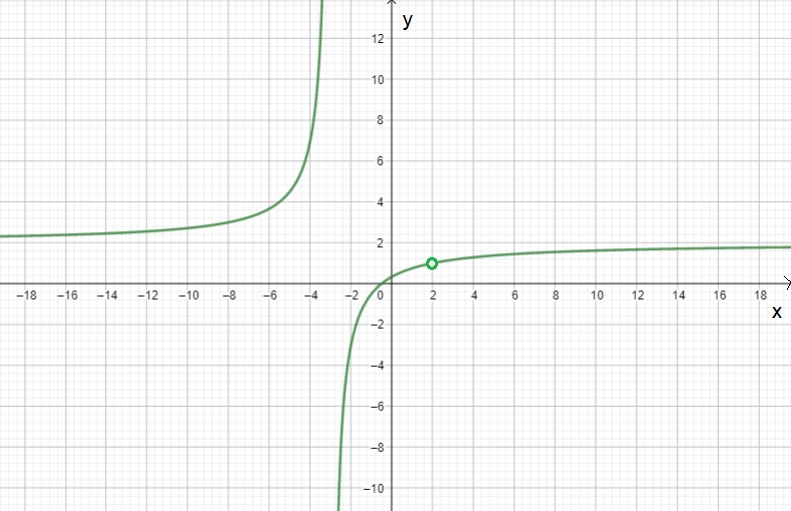
La función tiene una asíntota vertical de ecuación $x=-3$ .

Y una asíntota horizontal de ecuación $y=2$ , ya que $\underset{x\to \infty}{\lim}\frac{2x^2-3x-2}{x^2+x-6}=\underset{x\to \infty}{\lim}\frac{x^2(2-\frac{3}{x}-\frac{2}{x^2})}{x^2(1+\frac{1}{x}-\frac{6}{x^2})}=2$ y $\underset{x\to -\infty}{\lim}\frac{2x^2-3x-2}{x^2+x-6}=\underset{x\to -\infty}{\lim}\frac{x^2(2-\frac{3}{x}-\frac{2}{x^2})}{x^2(1+\frac{1}{x}-\frac{6}{x^2})}=2$.