Si el límite de la función cuando $x$ tiende a una constante (valores de $x$ que genere una división entre cero en la función) es igual a infinito positivo o negativo (aunque sea en forma lateral), entonces la función tiene una asíntota vertical de ecuación $x$ igual a la constante, esto es:
Si $\underset{x\to m}{\lim} \;f(x)=\infty$, $\underset{x\to m}{\lim} \;f(x)=-\infty$, o $\underset{x\to m}{\lim} \;f(x)=\not\exists $, con límites laterales infinitos.
Entonces $x=m$ es una asíntota vertical de $f(x)$.
($m$ es un valor de $x$ que genera una división entre cero en la función)
 |
 |
|---|---|
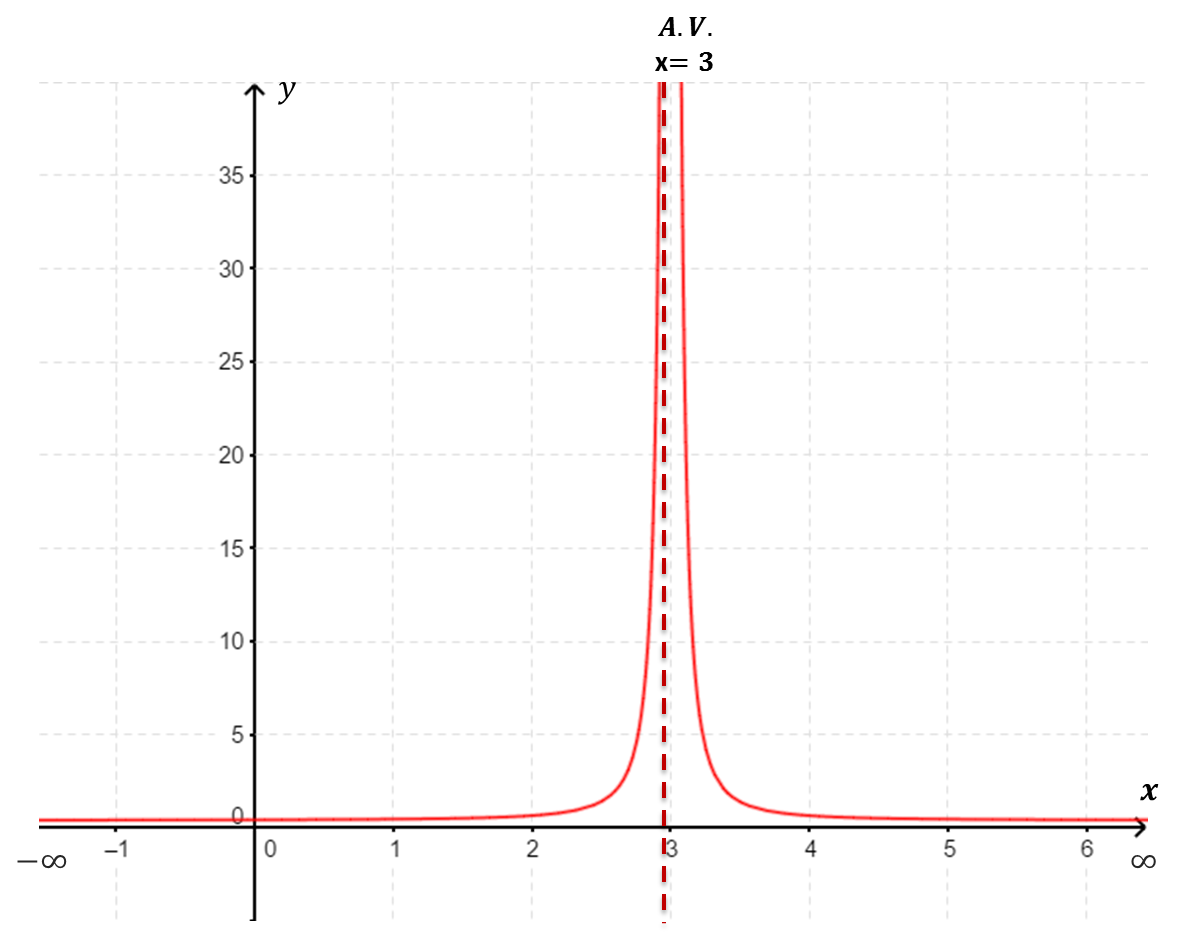
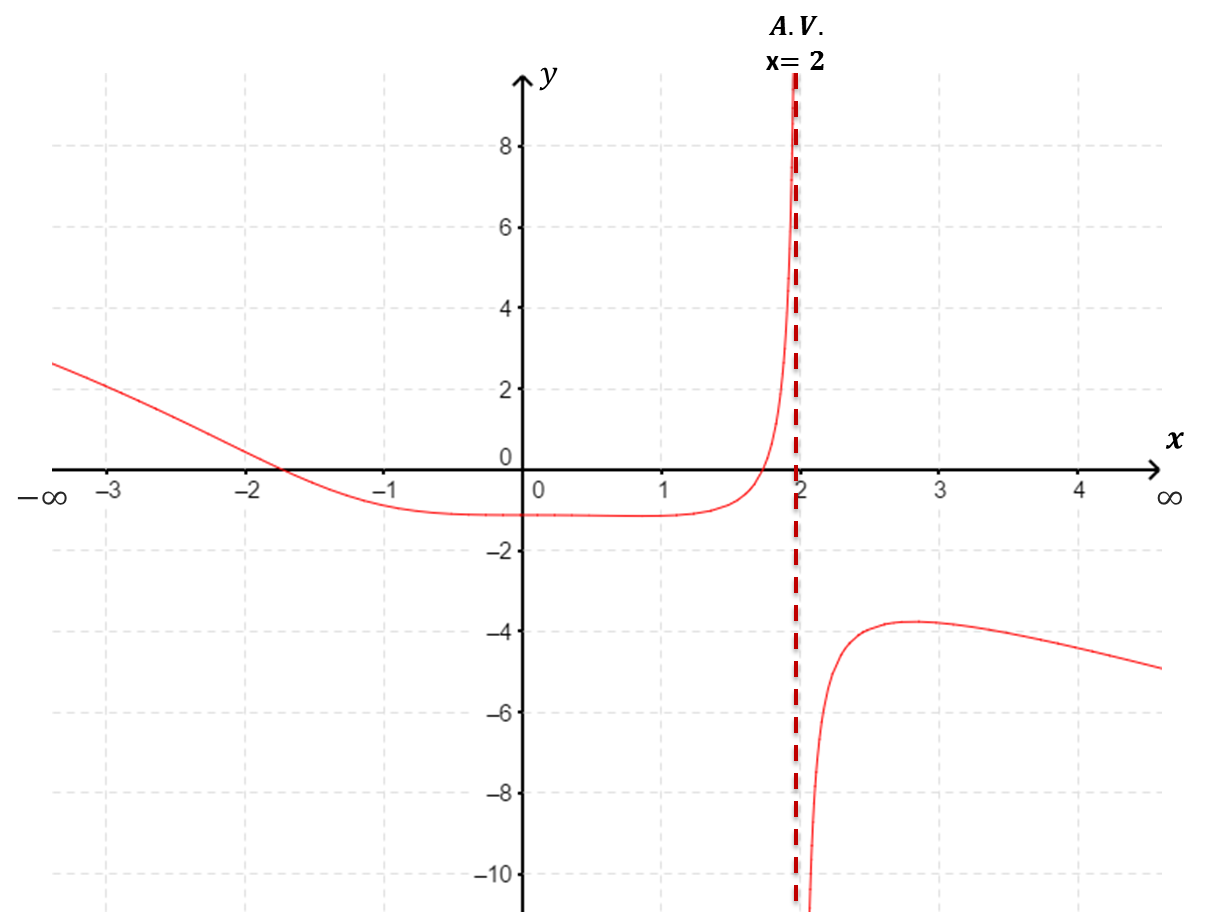
| $f(x)$ tiene una asíntota vertical de ecuación $x=3$ ( $\underset{x\to 3}{\lim} \;f(x)=\infty$). | $f(x)$ tiene una asíntota vertical de ecuación $x=2$ ( $\underset{x\to 2^{+}}{\lim} f(x)=-\infty$ y $\underset{x\to 2^{-}}{\lim} f(x)=\infty$). |
Hay que calcular el límite de la función cuando $x$ tiende al valor que genere una división entre cero en la función.
$$x+3=0$$
$$x=-3$$
$\underset{x \rightarrow -3}{\lim}\frac{x-2}{x+3}:\frac{-5}{0}$: infinito o menos infinito, hay que calcular límites laterales.
$\underset{x \rightarrow -3^-}{\lim}\frac{x-2}{x+3}=\frac{-5}{0^-}=\infty$ (un negativo entre un negativo da un positivo)
Sabemos que el denominador se va a cero tomando valores negativos porque si $x$ es menor que $-3$, $x<-3$ se tiene que $x+3<0$ (o evaluándolo en el primer entero a la izquierda de $-3$ que es el $-4$ queda $-4+3=-1$ un número negativo, que se acercará a $0$ cuando se tomen valores de $x$ más cerca de $-3$ por la izquierda).
$\underset{x \rightarrow -3^+}{\lim}\frac{x-2}{x+3}=\frac{-5}{0^+}=-\infty$ (un negativo entre un positivo da un negativo)
Sabemos que el denominador se va a cero tomando valores positivos porque si $x$ es mayor que $-3$, $x>-3$ se tiene que $x+3>0$ (o evaluándolo en el primer entero a la derecha de $-3$ que es el $-2$ queda $-2+3=1$ un número positivo, que se acercará a $0$ cuando se tomen valores de $x$ más cerca de $-3$ por la derecha).
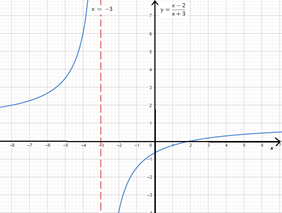
$f(x)=\frac {x-2}{x+3}$ tiene una asíntota vertical de ecuación $x=-3$. Y como los límites laterales son diferentes el $\underset{x \rightarrow -3}{\lim}\frac{x-2}{x+3}$ No existe.
Su gráfica es:
Hay que calcular el límite de la función cuando $x$ tiende al valor que genere una división entre cero en la función.
$$2x^2+x-10=0$$
$$2x^2+x-10=(2x+5)(x-2)=0$$
$x=-\frac{5}{2}=-2.5$ y $x=2$
Hay que calcular los límites cuando $x$ tiende a $-\frac{5}{2}$ y a $2$.
$\underset{x \rightarrow -\frac{5}{2}}{\lim}\frac{4x^2+12x+5}{2x^2+x-10}:\frac{25-30+5}{\frac{25}{2}-\frac{5}{2}-10}=\frac{0}{0}$: indeterminado, hay que factorizar.
$\underset{x \rightarrow -\frac{5}{2}}{\lim}\frac{4x^2+12x+5}{2x^2+x-10}$=$\underset{x \rightarrow -\frac{5}{2}}{\lim}\frac{(x+\frac{5}{2})(4x+2)}{(x+\frac{5}{2})(2x-4)}$=$\underset{x \rightarrow -\frac{5}{2}}{\lim}\frac{(2x+5)(2x+1)}{(2x+5)(x-2)}$=$\underset{x \rightarrow -\frac{5}{2}}{\lim}\frac{2x+1}{x-2}$=$\frac{-4}{-\frac{9}{2}}$=$\frac{8}{9}$
La función no tiene asíntota vertical en $x=-\frac{5}{2}$ porque el límite no resultó más o menos infinito y la gráfica tendrá un hueco de coordenadas $(-\frac{5}{2},\frac{8}{9})$.
Para calcular el límite cuando $x$ tiende a 2 podemos tomar la expresión de la función simplificada.
$\underset{x \rightarrow 2}{\lim}\frac{4x^2+12x+5}{2x^2+x-10}=\underset{x \rightarrow 2}{\lim}\frac{2x+1}{x-2}:\frac{5}{0}$: infinito o menos infinito, hay que calcular límites laterales.
$\underset{x \rightarrow 2^-}{\lim}\frac{2x+1}{x-2}=\frac{5}{0^-}=-\infty$ (un positivo entre un negativo da un negativo)
Sabemos que el denominador se va a cero tomando valores negativos porque si $x$ es menor que $2$, $x<2$ tendremos que $x-2<0$ (o evaluándolo en el primer entero a la izquierda de $2$ que es el $1$ queda $1-2=-1$ un número negativo, que se acercará a $0$ cuando se tomen valores de $x$ más cerca de $2$ por la izquierda).
$\underset{x \rightarrow 2^+}{\lim}\frac{2x+1}{x-2}=\frac{5}{0^+}=\infty$ (un positivo entre un positivo da un positivo)
Sabemos que el denominador se va a cero tomando valores positivos porque si $x$ es mayor que $2$, $x>2$ tendremos que $x-2>0$ (o evaluándolo en el primer entero a la derecha de $2$ que es el $3$ queda $3-2=1$ un número positivo, que se acercará a $0$ cuando se tomen valores de $x$ más cerca de $2$ por la derecha).
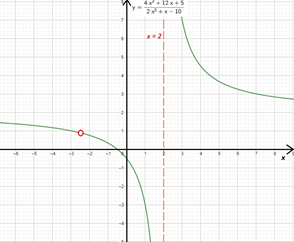
$f(x)=\frac{4x^2+12x+5}{2x^2+x-10}$ tiene únicamente una asíntota vertical de ecuación $x=2$. Y como los límites laterales son diferentes el $\underset{x \rightarrow 2}{\lim}\frac{2x+1}{x-2}$ No existe.
Su gráfica es:
Hay que calcular el límite de la función cuando $x$ tiende al valor que genere una división entre cero en la función.
$$\sqrt{x^2-4}=0$$
$$x^2-4=0$$
$$x^2=4$$
$$x=\pm 2$$
$\underset{x \rightarrow -2}{\lim}\frac{x}{\sqrt{x^2-4}}$: para evaluar este límite se debe tener cuidado con el $\underset{x \rightarrow -2}{\lim}\sqrt{x^2-4}$ ya que el resultado es $\sqrt{0}$ hay que verificar que el contenido del radical se acerque a cero tomando únicamente valores positivos, esto sucede nada más para valores $x$ menores que $-2$, así que sólo existe el límite lateral izquierdo.
Obsérvese que el dominio de la función es $D_f=(-\infty,-2)\cup(2,\infty)$.
$\underset{x \rightarrow -2^-}{\lim}\frac{x}{\sqrt{x^2-4}}=\frac{-2}{\sqrt{0^+}}=\frac{-2}{0^+}=-\infty$ (un negativo entre un positivo da un negativo)
La función tiene una asíntota vertical de ecuación $x=-2$.
Análogamente en el límite de la función cuando x tiende a 2, sólo existe el límite lateral derecho.
$$\underset{x \rightarrow 2^+}{\lim}\frac{x}{\sqrt{x^2-4}}=\frac{2}{\sqrt{0^+}}=\frac{2}{0^+}=\infty$$
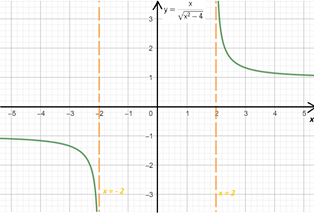
La función tiene otra asíntota vertical de ecuación $x=2$.
Su gráfica es:
Si el límite de la función cuando $x$ tiende a infinito o menos infinito es igual a una constante, entonces la función tiene una asíntota horizontal de ecuación: $y$ igual a la constante, esto es:
Si $\underset{x\to-\infty}{\lim} f(x)=k$ entonces $y=k$ es una asíntota horizontal de $f(x)$.
Si $\underset{x\to\infty}{\lim} \;f(x)=p$ entonces $y=p$ es una asíntota horizontal de $f(x)$.
 |
 |
|---|---|
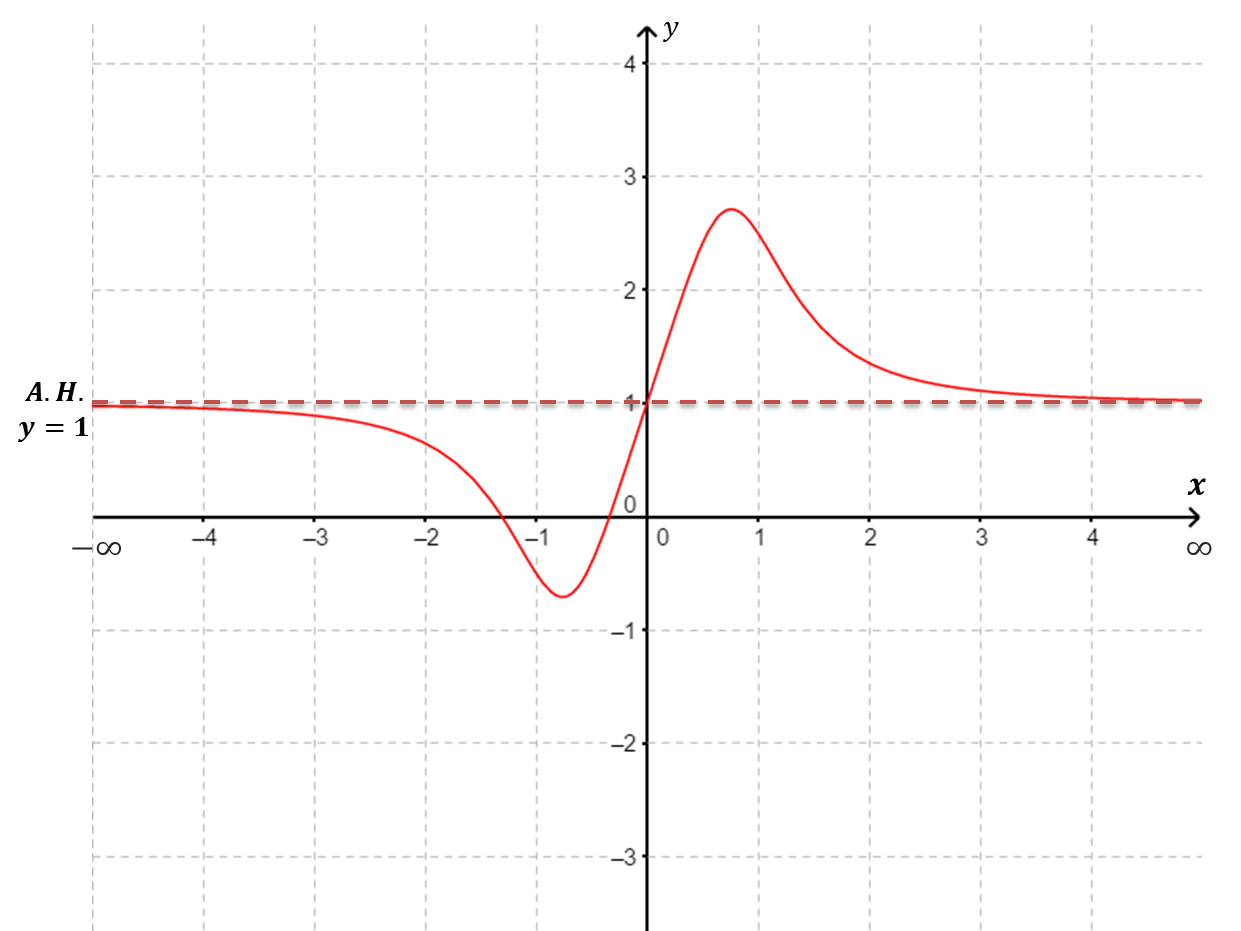
| $f(x)$ tiene una asíntota horizontal de ecuación $y=1$ $\underset{x\to \infty}{\lim} f(x)=1$ y $\underset{x\to -\infty}{\lim} f(x)=1$. |
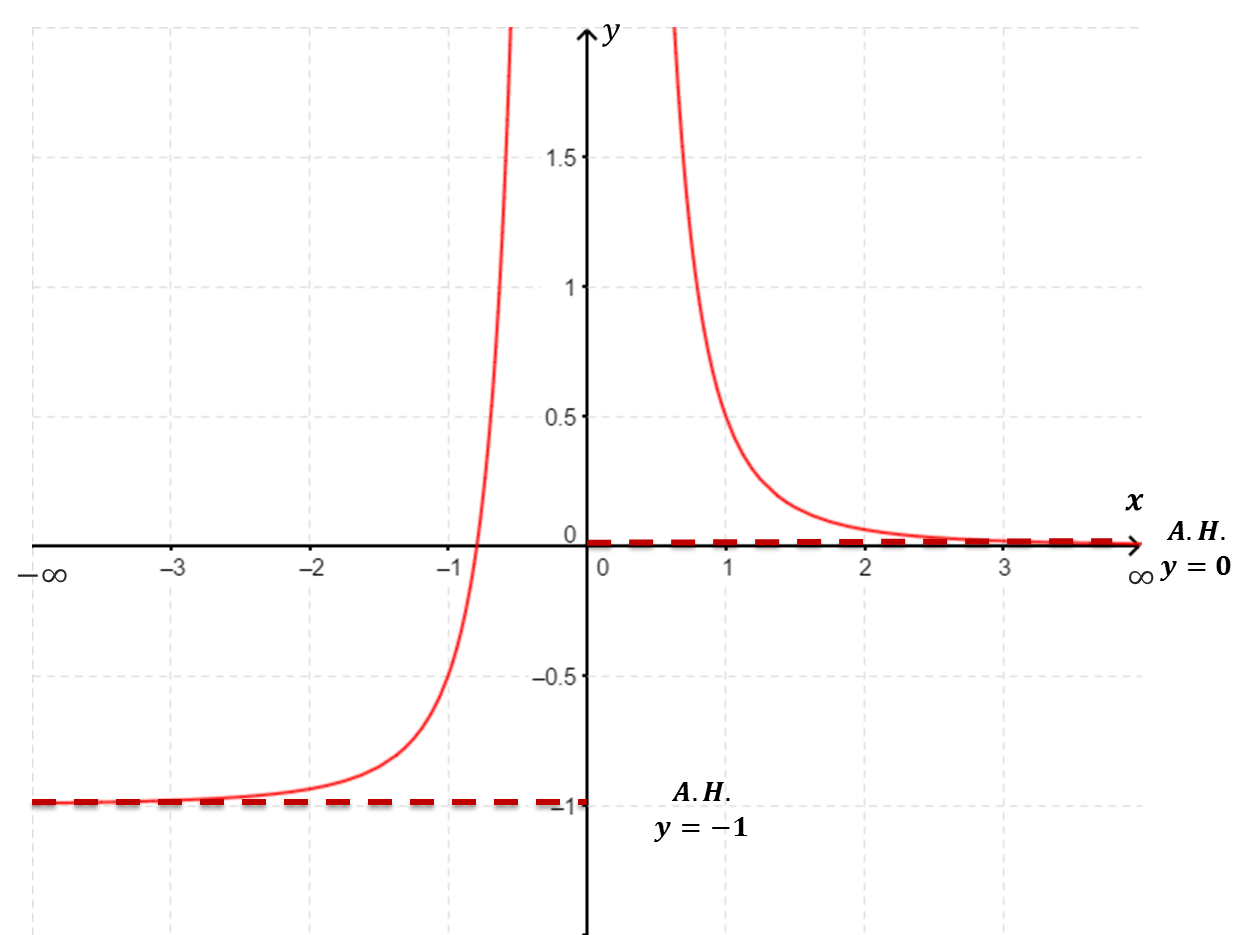
$f(x)$ tiene 2 asíntotas horizontales de ecuaciones $y=-1$ y $y=0$ $\underset{x\to \infty}{\lim} f(x)=0$ y $\underset{x\to -\infty}{\lim} f(x)=-1$. |
Hay que calcular el límite de la función cuando $x$ tiende a infinito y a menos infinito.
$\underset{x \rightarrow \infty}{\lim}\frac{x-2}{x+3}:\frac{\infty}{\infty}$: indeterminado, se factoriza forzadamente la $x$ de mayor de potencia.
$$\underset{x \rightarrow \infty}{\lim}\frac{x(1-\frac{2}{x})}{x(1+\frac{3}{x})}=\underset{x \rightarrow \infty}{\lim}\frac{1-\frac{2}{x}}{1+\frac{3}{x}}=\frac{1-0}{1+0}=1$$
y análogamente
$$\underset{x \rightarrow -\infty}{\lim}\frac{x-2}{x+3}=1$$
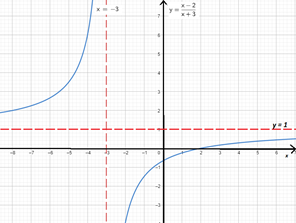
La función tiene una asíntota horizontal de ecuación $y=1$.
Su gráfica es:
Hay que calcular el límite de la función cuando $x$ tiende a infinito y a menos infinito.
$\underset{x \rightarrow \infty}{\lim}\frac{4x^2+12x+5}{2x^2+x-10}:\frac{\infty}{\infty}$: indeterminado, se factoriza forzadamente la $x$ de mayor de potencia.
$$\underset{x \rightarrow \infty}{\lim}\frac{x^2(4+\frac{12}{x}+\frac{5}{x^2})}{x^2(2+\frac{1}{x^2}-\frac{10}{x})}=\underset{x \rightarrow \infty}{\lim}\frac{4+\frac{12}{x}+\frac{5}{x^2}}{2+\frac{1}{x^2}-\frac{10}{x}}=\frac{4+0+0}{2+0-0}=2$$
y análogamente
$$\underset{x \rightarrow -\infty}{\lim}\frac{4x^2+12x+5}{2x^2+x-10}=2$$
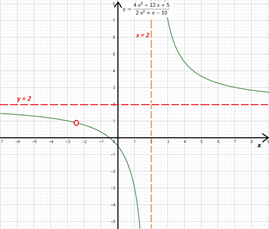
La función tiene una asíntota horizontal de ecuación $y=2$.
Su gráfica es:
Hay que calcular el límite de la función cuando $x$ tiende a infinito y a menos infinito.
$\underset{x \rightarrow \infty}{\lim}\frac{x}{\sqrt{x^2-4}}:\frac{\infty}{\infty}$: indeterminado, se factoriza forzadamente la $x$ de mayor de potencia.
$$\underset{x \rightarrow \infty}{\lim}\frac{x}{\sqrt{x^2(1-\frac{4}{x^2})}}=\underset{x \rightarrow \infty}{\lim}\frac{x}{|x|\sqrt{1-\frac{4}{x^2}}}=\underset{x \rightarrow \infty}{\lim}\frac{x}{x\sqrt{1-\frac{4}{x^2}}}=\underset{x \rightarrow \infty}{\lim}\frac{1}{\sqrt{1-\frac{4}{x^2}}}=\frac{1}{\sqrt{1-0}}=1$$
Notese que $|x|=x$ si $x\rightarrow\infty$ y que $|x|=-x$ si $x\rightarrow-\infty$. Asi que
$$\underset{x \rightarrow -\infty}{\lim}\frac{x}{\sqrt{x^2(1-\frac{4}{x^2})}}=\underset{x \rightarrow -\infty}{\lim}\frac{x}{|x|\sqrt{1-\frac{4}{x^2}}}=\underset{x \rightarrow -\infty}{\lim}\frac{x}{-x\sqrt{1-\frac{4}{x^2}}}=\underset{x \rightarrow -\infty}{\lim}\frac{1}{-\sqrt{1-\frac{4}{x^2}}}=\frac{1}{-\sqrt{1-0}}=-1$$
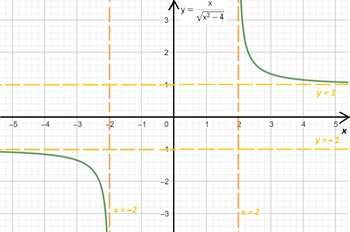
La función $f(x)=\frac{x}{\sqrt{x^2-4}}$ tiene dos asíntotas horizontales una de ecuación $y=1$ por el lado derecho del eje $x$ y otra de ecuación $y=-1$ por el lado izquierdo del eje $x$.
Su gráfica es: