Funciones como Modelos Matemáticos

Para modelar matemáticamente algunos problemas de situaciones reales o geométricos se utilizan las funciones, por ejemplo:

Expresar mediante una función de una variable, el perímetro de un terreno rectangular que tiene área de 24 $m^2$.

1. El primer punto es entender el problema, se recomienda hacer un esquema y dar nombre a las variables involucradas.

   

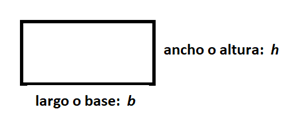
2. Expresar la información que se da en el problema, en términos de las variables definidas.
                           Área 24 $m^2$
   
                           Tomamos nota que todas las longitudes
                           se trabajarán en metros y suprimimos su
                           referencia en los desarrollos.
   
                                             $A=24=bh$
   
   
3. Expresar lo que se pide en el problema en términos de las variables definidas y resolver.
                           Perímetro como función de una variable.
   
                                             $P=2b+2h$   (dos variables)
   
                           Se busca una relación entre ellas, en este caso del área:
   
                                             $bh=24$   de donde
   
                                             $b=\frac{24}{h}$   y substituimos en P
   
                                             $P=2(\frac{24}{h})+2h$   simplificamos
   
                                             $P=\frac{48}{h}+2h$
   
   Ya se tiene la función, perímetro, como función de una variable, la altura.
   
   

Ejemplo 2

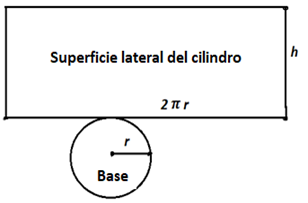
Un envase cilíndrico, sin tapa, contiene 2 $dm^3$ de agua, expresar el área superficial del envase como función de su radio.

1. Hacer un esquema y referenciar las variables involucradas.

   

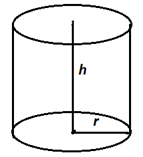
2. Expresar la información que se da en el problema, en términos de las variables definidas.
                                             Volumen $2$ $dm^3$
   
                                             $V=2=\pi r^2 h$
   
   
3. Expresar lo que se pide en el problema en términos de las variables definidas y resolver.
   
   
   Área superficial como función del radio.
   
   El área superficial es la suma del área del círculo más la del rectángulo cuyo largo es el perímetro del círculo.
   
   $AS=\pi r^2+2\pi rh$ (dos variables)
   
   Del volumen se tiene que $$\pi r^2 h=2$$ despejando, $$h=\frac{2}{\pi r^2}$$ y se substituye, $$AS=\pi r^2+2\pi r\left(\frac{2}{\pi r^2}\right)$$ simplificando $$AS(r)=\pi r^2+\frac{4}{r}$$
      
   
   Ya se tiene el área superficial del envase como función del radio.