


El Esbozo gráfico de una función es la representación gráfica aproximada de la función en un sistema de ejes coordenados, es decir, el conjunto de todos los puntos coordenados $(x,y)$ definidos por la función $y=f(x)$.
Un buen esbozo gráfico debe mostrar los puntos donde la gráfica tiene algún cambio de comportamiento, ajustando la escala de forma conveniente.
De manera general, para hacer el esbozo gráfico se toma en cuenta la información que se pueda obtener analíticamente y se complementa obteniendo algunos de sus puntos coordenados evaluando la función, es decir, dar algunos valores para $x$ y calcular los valores correspondientes de $y$, lo que se llama comúnmente tabular la función.
Conforme se conozcan más elementos de la función, obtenidos analíticamente, se necesitarán menos tabulaciones para tener un buen esbozo gráfico.
| $f(x)=\sqrt[]{5-2x}$ | $g ( x )$ = $-\sqrt[]{2x^2-18}$ | $j ( x )$ = $\frac{2x}{3x^2-12}$ |
|---|---|---|
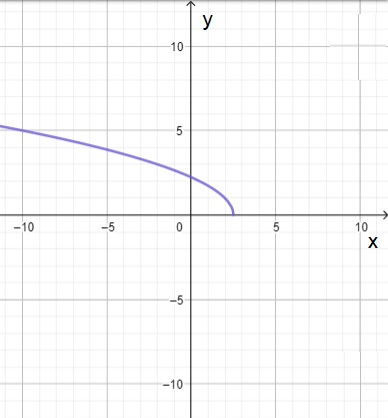 |
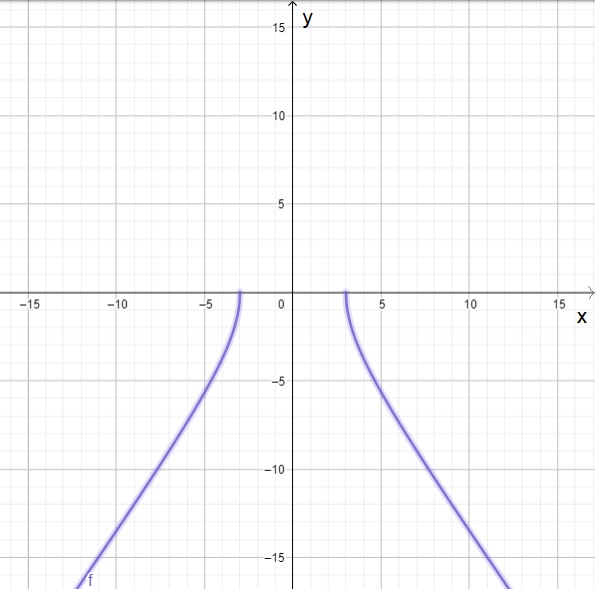 |
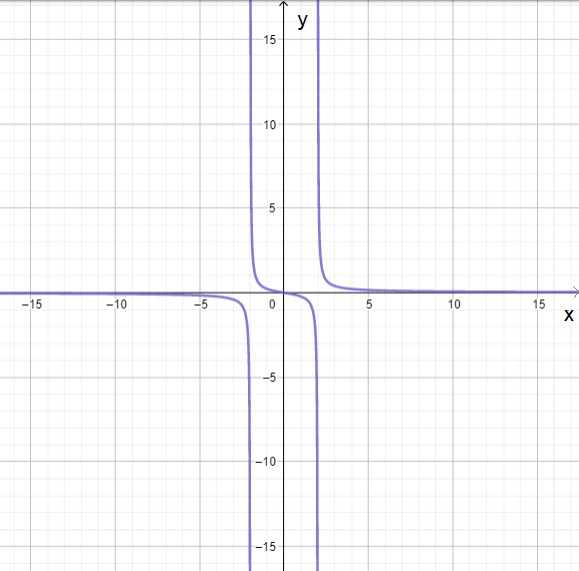 |
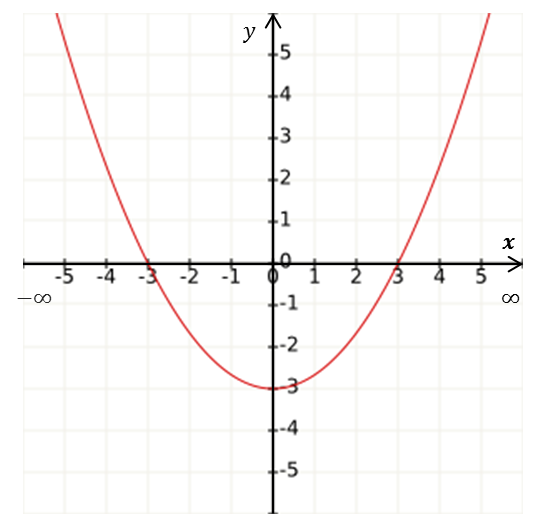
El rango (o contradominio) de la función $y =f(x)$ es el conjunto de todas las imágenes, esto es, el conjunto de todos los valores de la variable $y$ que están asociadas a algún valor de $x.$
 |
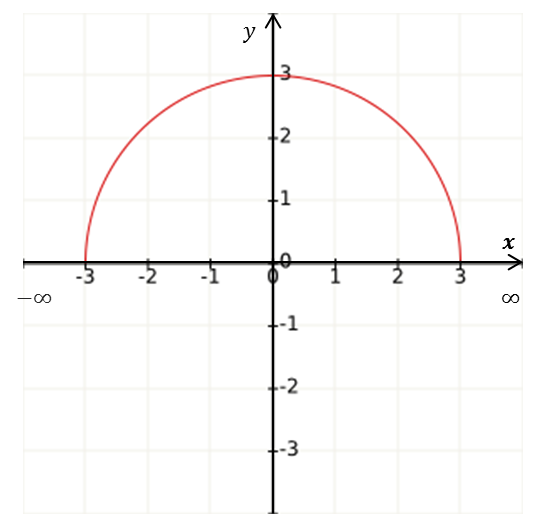 |
|---|---|
| El rango es el conjunto de todas las $y\in[-3,\infty)$ | El rango es el conjunto de todas las $y\in[0,3]$ |
Gráficamente el rango son los valores de $y$ asociados a los valores de $x$, esto es, los intervalos en el eje $y$ donde hay gráfica.
| $f(x)=\sqrt[]{5-2x}$ | $g ( x )$ = $-\sqrt[]{2x^2-18}$ | $j ( x )$ = $\frac{2x}{3x^2-12}$ |
|---|---|---|
 |
 |
 |
| El rango de $f(x)=\sqrt[]{5-2x}$ es el conjunto de todas las $y\in[0,\infty)$ | El rango de $g ( x )$ = $-\sqrt[]{2x^2-18}$ es el conjunto de todas las $y\in(-\infty,0]$ | El rango de $j ( x )$ = $\frac{2x}{3x^2-12}$ es el conjunto de todas las $y\in(-\infty,\infty)$ |