Funciones

En general una función es una regla o forma de asociar elementos de un conjunto con elementos de otro conjunto, de tal manera que a un elemento del primer conjunto le corresponda sólo un elemento del segundo conjunto.

Cuando los dos conjuntos son de números reales se tiene una función real de variable real que suele denotarse como  $y = f ( x )$, donde  $x$ está en el primer conjunto  y  se le llama variable independiente y  $y$  está en el segundo conjunto y se le llama variable dependiente o función.

Por ejemplo la función: todo número asociado con su doble, así el  $1.3$  quedará asociado con el  $2.6$;  el $–1$  con el  $–2$; etc.

Se denotará la función como  $y = f ( x ) = 2 x$

y se tiene que  $y = f ( 1.3 ) = 2(1.3)=2.6$;

                      $y= f ( -1 ) = 2(-1)=- 2$; etc.

Y se pueden representar gráficamente, en un sistema de ejes coordenados $x-y$ como puntos.

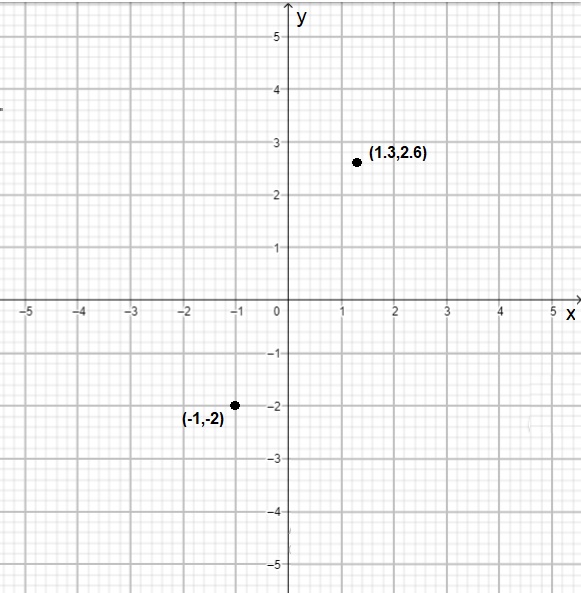
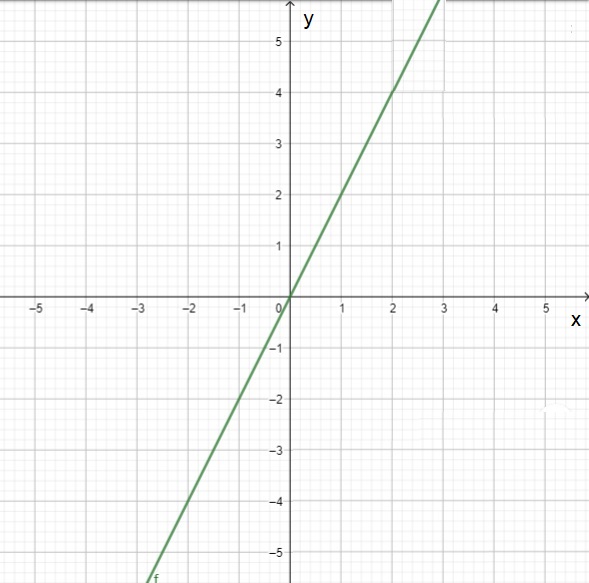
Todas las posibles asociaciones nos darán la gráfica de la función.

Dominio

El dominio de una función (real de variable real)  $y=f(x)$, es el conjunto de valores de  $x$  para los que la función puede dar una imagen:  $y$,  es decir,  $f(x)$ puede ser evaluada en un número real  $x$  y producir a su vez otro número real  $y=f(x)$.

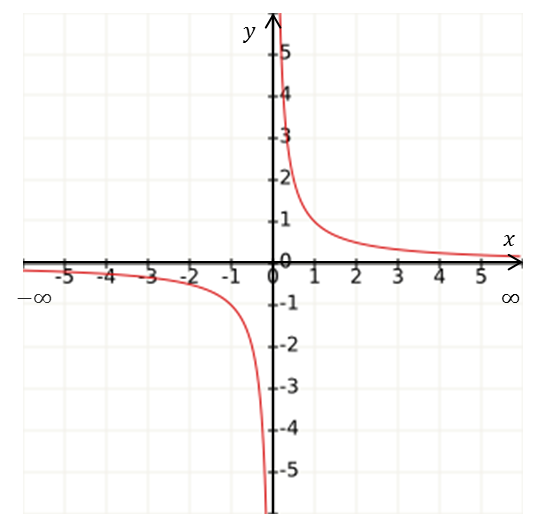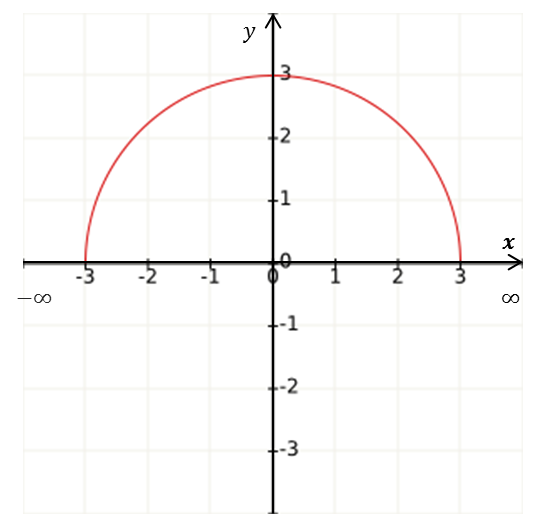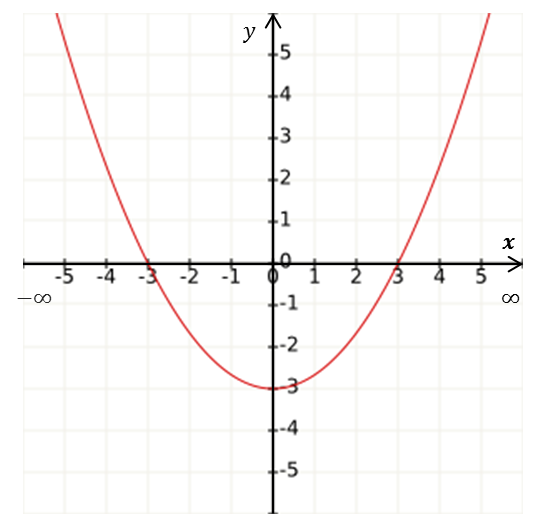
$D_f=(-\infty,\infty)$	$D_f=(-\infty,0)\cup(0,\infty)$	$D_f=[-3,3]$

Gráficamente son los valores de  $x$  que tienen una  $y$  asociada, esto es, los intervalos del eje  $x$  donde hay gráfica.

Para obtener el dominio de una función recordamos que de manera general, en expresiones del tipo:

1. $\frac{a}{b}$  debe satisfacerse que  $b\neq 0$  (en expresiones racionales el denominador debe ser diferente de cero).
   
   
2. $\sqrt[2n]{c}$ debe satisfacerse que  $c\geq0$  (en radicales pares como raíz cuadrada, raíz cuarta, etc. Su contenido debe ser mayor o igual que cero, para que el resultado esté en los números reales).

Ejemplo 1

Obtener el dominio de $f ( x )$ = $\sqrt[]{5-2x}$.

El dominio de la función $y=f ( x )$ = $\sqrt[]{5-2x}$ debe satisfacer que $5-2x\geq0$, para que $y$ esté en los números reales, es decir, son todos los reales tales que:

$$5-2x\geq 0$$ $$5\geq 2x$$ $$2x\leq 5$$ $$x\leq \frac{5}{2}$$ $$x\in(-\infty,\frac{5}{2}] $$ de esta manera el dominio de $f(x)$ se escribe como:

$$D_f=(-\infty,\frac{5}{2}], $$
ya que para esos valores de  $x$  se puede obtener un valor de  $y$ en los reales.

Ejemplo 2

Obtener el dominio de $g ( x )$ = $-\sqrt[]{2x^2-18}$.

El dominio de la función $y=g ( x )$ = $-\sqrt[]{2x^2-18}$ debe satisfacer que $2x^2-18\geq0$, para que $y$ esté en los números reales, es decir, son todos los reales tales que:

$$2x^2-18\geq 0$$ $$2x^2\geq 18$$ $$x^2\geq 9$$ $$ \sqrt[]{x^2}\geq \sqrt[]{9}$$ $$|x|\geq 3$$ $$x\geq3\;\;\;\; o\;\;\;\; x\leq -3$$ $$x\in(-\infty,-3]\cup[3,\infty) $$ de esta manera el dominio de $g(x)$ se escribe como:

$$D_g=(-\infty,-3]\cup[3,\infty), $$
ya que para esos valores de  $x$  se puede obtener un valor de  $y$ en los reales.

Ejemplo 3

Obtener el dominio de $h ( x )$ = $\frac{3x^2-x-14}{2x^2+7x+6}$.

El dominio de la función $y=h ( x )$ = $\frac{3x^2-x-14}{2x^2+7x+6}$ debe satisfacer que $2x^2+7x+6\neq0$, para que $y$ esté en los números reales, es decir, $y$ no existe cuando:

$$2x^2+7x+6 = 0$$ $$(2x+3)(x+2)=0$$                                        $2x+3 = 0$          y           $x+2=0$

                                            $x = -\frac{3}{2}$          y           $x=-2$

de esta manera el dominio de $h(x)$ se escribe como:

$$D_h=(-\infty,-2)\cup(-2,-\frac{3}{2})\cup(-\frac{3}{2},\infty), $$
ya que para esos valores de  $x$  se puede obtener un valor de  $y$ en los reales.

Raíces o ceros

Las raíces o ceros de una función son los valores en el dominio cuya imagen es cero, esto es si $y=f(x)$, las raíces o ceros de la función son los valores de $x$ que hacen  $y=f(x)=0$  con  $x\in D_{f}$. Y se denota como  $C_f=\{x_1, x_2, ....\}$.

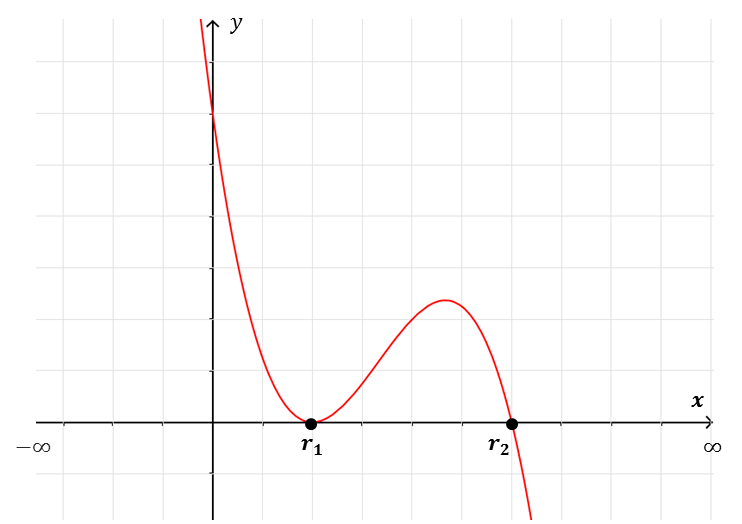
                                                            $f(r_1)=0$       $f(r_2)=0$      $C_f=\{r_1, r_2\}$

Gráficamente las raíces reales se identifican como la abscisa (valor de  $x$) de los puntos donde la gráfica toca o corta al eje  $x$.

Ejemplo 1

Obtener las raíces de $f ( x )$ = $\sqrt[]{5-2x}$.

Las raíces o ceros de $y=f ( x )$ = $\sqrt[]{5-2x}$ son los valores en el dominio cuya imagen es cero, esto es:

$$\sqrt[]{5-2x}=0$$ $$5-2x=0$$ $$2x=5$$ $$x=\frac{5}{2}$$ Como $x=\frac{5}{2}$ $\in D_{f}$ entonces es raíz de $f(x)$. $C_f=\{\frac{5}{2}\}$

Ejemplo 2

Obtener las raíces de $g ( x )$ = $-\sqrt[]{2x^2-18}$.

Las raíces o ceros de $y=g ( x )$ = $-\sqrt[]{2x^2-18}$ son los valores en el dominio cuya imagen es cero, esto es:

$$-\sqrt[]{2x^2-18}=0$$ $$2x^2-18=0$$ $$2x^2=18$$ $$x^2=9$$ $$ \sqrt[]{x^2}= \sqrt[]{9}$$ $$|x|=3$$ Como $x=-3$ y $x=3$ $\in D_{g}$ entonces son raíces de $g(x)$. $C_g=\{-3, 3\}$

Ejemplo 3

Obtener las raíces de $h ( x )$ = $\frac{3x^2-x-14}{2x^2+7x+6}$.

Las raíces o ceros de $y$ = $h ( x )$ = $\frac{3x^2-x-14}{2x^2+7x+6}$ son los valores en el dominio cuya imagen es cero, esto es:

$$\frac{3x^2-x-14}{2x^2+7x+6}=0$$ $$3x^2-x-14=0$$ $$(3x-7)(x+2)$$                                        $3x-7 = 0$          y           $x+2=0$

                                            $x = \frac{7}{3}$          y           $x=-2$

Como $x=-2$ $\not\in D_{h}$ entonces $x=\frac{7}{3}$ es la única raíz de $g(x)$. $C_h=\{\frac{7}{3}\}$

Paridad

La paridad de una función puede verse como una especificación de simetría de su gráfica, la definición es la siguiente.

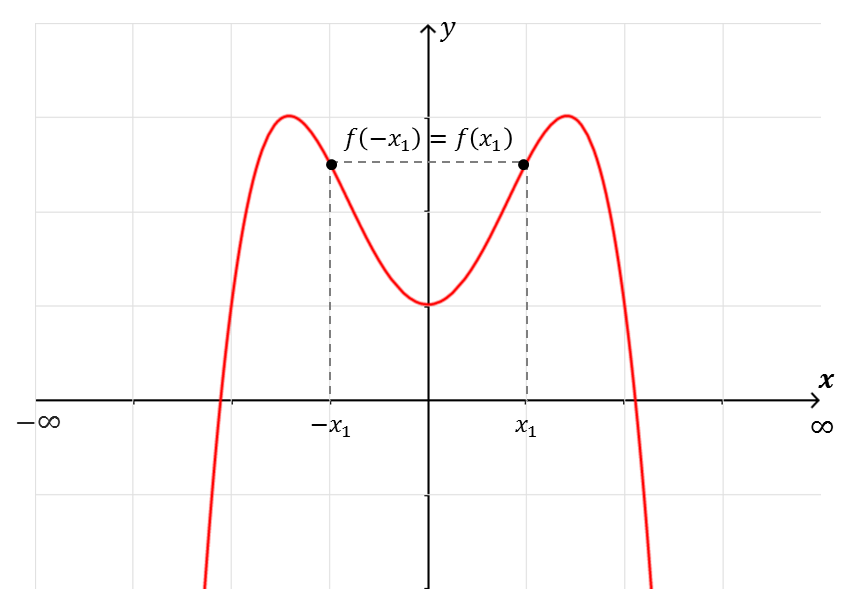
1. $\boldsymbol{f(x)}$  es una función par; si  $f(-x)=f(x)$  para toda  $x\in D_f$,  esto es, la función da la misma imagen a un valor de  $x$  que a su negativo  $-x$.

   Su gráfica tiene simetría con respecto al eje  $y$  (si se doblara la gráfica en el eje  $y$,  las dos partes coincidirían).

2. $\boldsymbol{f(x)}$  es una función impar; si  $f(-x)=-f(x)$  para toda  $x\in D_f$  esto es, la función da el negativo de la imagen de un valor  $x$,  a su valor negativo  $-x$.

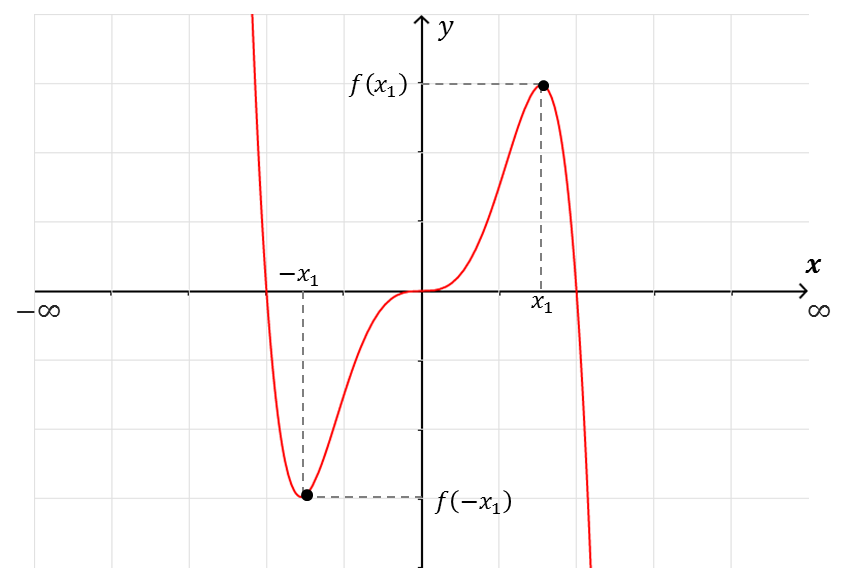   $f(-x_1)=-f(x_1)$

   Su gráfica tiene simetría con respecto al origen (cualquier recta que pase por el origen, corta a la gráfica de la misma forma de un lado del origen, que del otro, esto es, a la misma distancia y en el mismo número de puntos).

3. $\boldsymbol{f(x)}$  no tiene paridad; cuando no se satisface ninguna de las dos condiciones anteriores. Su gráfica no tiene simetría con respecto al eje  $y$  o al origen.

Encontrar la paridad de una función es importante, puesto que si la función por analizar resulta ser par o impar, bastará con analizarla para valores positivos y cero de  $x$  y por el tipo de simetría se puede concluir para los valores negativos.

Ejemplo 1

Obtener la paridad de $f ( x )$ = $\sqrt[]{5-2x}$.

La paridad de $f$ se obtiene al evaluar $f (- x )$ y verificar cual de los 3 casos arriba mencionados satisface. $$f ( x ) = \sqrt[]{5-2x}$$ $$f (- x ) = \sqrt[]{5-2(-x)}=\sqrt[]{5+2x}$$ $$-f(x)= -\sqrt[]{5-2x}$$ $f(-x)\neq f(x)$, $ f(x) $ no es par y $f(-x)\neq -f(x)$, $ f(x)$ no es impar, por lo tanto la función $f(x)$ no tiene paridad, la gráfica de la función no es simétrica con respecto al eje $y$, y tampoco con respecto al origen.

Ejemplo 2

Obtener la paridad de $g ( x )$ = $-\sqrt[]{2x^2-18}$.

La paridad de $g$ se obtiene al evaluar $g (- x )$ y verificar cual de los 3 casos arriba mencionados satisface. $$g ( x ) = -\sqrt[]{2x^2-18}$$ $$g (-x ) = -\sqrt[]{2(-x)^2-18}=-\sqrt[]{2x^2-18}$$ Como $g(-x)= g(x)$ entonces $g(x)$ es una función par, la gráfica es simétrica con respecto al eje $y$.

Ejemplo 3

Obtener la paridad de $h ( x )$ = $\frac{3x^2-x-14}{2x^2+7x+6}$.

La paridad de $h$ se obtiene al evaluar $h (- x )$ y verificar cual de los 3 casos arriba mencionados satisface. $$h ( x ) = \frac{3x^2-x-14}{2x^2+7x+6}$$ $$h ( -x ) = \frac{3(-x)^2-(-x)-14}{2(-x)^2+7(-x)+6}=\frac{3x^2+x-14}{2x^2-7x+6}$$ $$-h ( x ) = -\frac{3x^2-x-14}{2x^2+7x+6}$$ $h(-x)\neq h(x)$, $ h(x) $ no es par y $h(-x)\neq -h(x)$, $ h(x)$ no es impar, por lo tanto la función $h(x)$ no tiene paridad, la gráfica de la función no es simétrica con respecto al eje $y$, y tampoco con respecto al origen.

Ejemplo 4

Obtener la paridad de $j ( x )$ = $\frac{2x}{3x^2-12}$.

La paridad de $j$ se obtiene al evaluar $j (- x )$ y verificar cual de los 3 casos arriba mencionados satisface. $$j ( x ) = \frac{2x}{3x^2-12}$$ $$j ( -x ) = \frac{2(-x)}{3(-x)^2-12}=\frac{-2x}{3x^2-12}=-\frac{2x}{3x^2-12}$$ $$-j ( x ) = -\frac{2x}{3x^2-12}$$ Como $j(-x)= -j(x)$ entonces $j(x)$ es una función impar, la gráfica es simétrica con respecto al origen.

Punto de corte eje $y$

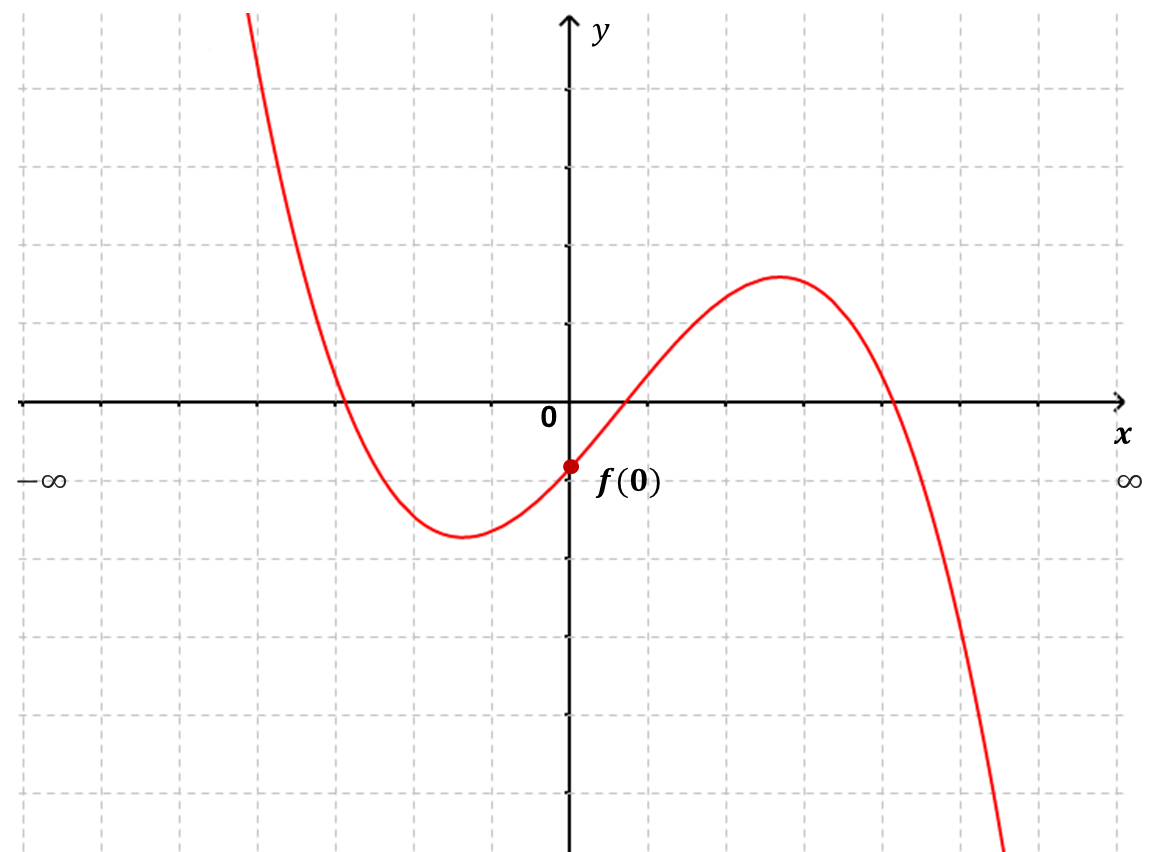
Punto de corte al eje $y$: El punto donde la gráfica de la función $y=f(x)$ corta al eje $y$ es la evaluación de la función en $x=0$, esto es $y=f(0)$.

Ejemplo 1

Obtener el punto de corte al eje $y$ de $f ( x )$ = $\sqrt[]{5-2x}$.

El punto donde la gráfica de la función $y=f ( x )$ = $\sqrt[]{5-2x}$ corta al eje $y$ es la evaluación de la función en $x=0$, esto es:

$$f ( 0 ) = \sqrt[]{5-2(0)}$$ $$f ( 0 ) = \sqrt[]{5}$$ Por lo tanto el punto de corte al eje $y$ se da en $y=\sqrt[]{5}$.

Ejemplo 2

Obtener el punto de corte al eje $y$ de $g ( x )$ = $-\sqrt[]{2x^2-18}$.

El punto donde la gráfica de la función $y=g ( x )$ = $-\sqrt[]{2x^2-18}$ corta al eje $y$ es la evaluación de la función en $x=0$, como $x=0\not\in D_g$ entonces la función no intersecta en ningún punto al eje $y$.

Ejemplo 3

Obtener el punto de corte al eje $y$ de $h ( x )$ = $\frac{3x^2-x-14}{2x^2+7x+6}$.

El punto donde la gráfica de la función $y=h ( x )$ = $\frac{3x^2-x-14}{2x^2+7x+6}$ corta al eje $y$ es la evaluación de la función en $x=0$, esto es:

$$h ( 0 ) = \frac{3(0)^2-(0)-14}{2(0)^2+7(0)+6}$$ $$h ( 0 ) = \frac{-14}{6}=-\frac{7}{3}$$ Por lo tanto el punto de corte al eje $y$ se da en $y=-\frac{7}{3}$.