Funciones definidas por intervalos

Se dijo anteriormente que una función es una regla o forma de asociar elementos de un conjunto con elementos de otro conjunto, de tal manera que a un elemento del primer conjunto le corresponda sólo un elemento del segundo conjunto.

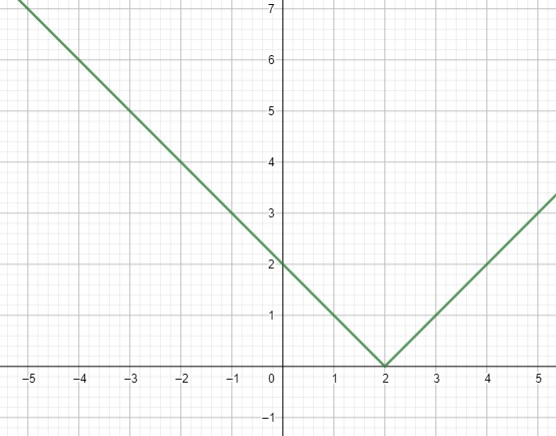
En funciones reales de variable real esa regla o forma de asociar los elementos, normalmente se expresa mediante una expresión algebraica, como $y = f(x)=3 x – 6$ y la función queda definida en todos los reales. Pero hay funciones como las de valor absoluto en que la regla cambia en los diferentes intervalos a considerar, por ejemplo en $f(x)=|x-2|$.

Ejemplo 1

Obtener el dominio, ceros o raíces, paridad, esbozo gráfico, rango, monotonía y signo de la función $f ( x )=|x-2|$.

      Dominio: $ D_f = (-\infty,\infty)$.

      Ceros o raíces: en $x=2$.

      Paridad: No tiene paridad.

      Esbozo gráfico:

$f(x)=|x-2|=\left\{\begin{matrix} x-2 & si & x-2 ≥ 0\\ & & x ≥ 2: [2,\infty) \\ \\ -(x-2) & si & x-2 < 0\\ & & x < 2: (-\infty,2) \end{matrix}\right.$

     Rango: $R_f=[0,\infty)$.
     Monotonía: $f(x)$ es decreciente para: $x\in(-\infty,2]$
                       $f(x)$ es creciente para: $x\in[2,\infty)$
     Signo de la función: $f(x)>0$ en $x\in(-\infty,2)\cup(2,\infty)$, $f(x)$ nunca es negativa.

En las funciones definidas por intervalos la regla cambia en los diferentes intervalos a considerar, por ejemplo: $y=f(x)=x^2-4x$ para $x < 3$ o sea en el intervalo $(-\infty ,3 )\;\;\;$ y $\;\;\;y=f(x)=4$ para $3≤x≤6$ esto es en el intervalo $[ 3 , 6 ]$ lo que se denota como:

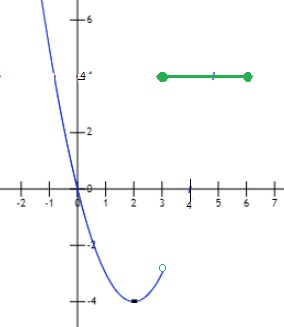
$f(x)=\left\{\begin{matrix} x^2-4x & si & x <3 \\ 4 & si & 3 ≤ x ≤ 6 \end{matrix}\right.$



• El dominio de la función es: $D_f=(-\infty,3 )∪[ 3 ,6 ]=(-\infty ,6 ]$.
  Como la función es sencilla se puede pasar a la gráfica. La $f(x)=x^2-4x=x(x-4)$ es una parábola que abre hacia arriba y tiene raíces en $x=0$ y $x=4$ vértice en $(x_v=\frac{-b}{2a}\;\;;\;\; y_v=f(x_v ) )$ esto es $x_v=2$ $y_v=f(2)=-4$ punto de coordenadas $( 2 , – 4 )$ y se toma la parte correspondiente al intervalo $(-\infty ,3 )$ en el eje $x$ y $f(x)=4$ es función constate, cuya gráfica es una recta horizontal que corta al eje $y$ en $4$ y se tomará la parte correspondiente al intervalo $[ 3 ,6 ]$ del eje $x$, el esbozo gráfico de $f(x)$ es:

  




• Ceros o raíces: $f(x)=0$ para $x=0$ únicamente, porque $x=4$ no entra en el intervalo correspondiente, es la que se ve en la gráfica, que es el punto donde la gráfica corta al eje $x$.



• Paridad: no tiene, ya que la gráfica no tiene simetría con respecto al eje y (no es par) y tampoco con respecto al origen (no es impar).



• Rango: $R_f=[-4 ,\infty)$ son todos los valores de y de la gráfica, el conjunto de imágenes.



• Monotonía:
  $\;\;\;f(x)$ decrece (la gráfica baja, vista de izquierda a derecha, como lo señala el sentido del eje $x$) para $x ∈ (-\infty ,2]$;
  $\;\;\;f(x)$ crece (la gráfica sube, vista de izquierda a derecha, como lo señala el sentido del eje $x$) para $x ∈[ 2 ,3 )$ y
  $\;\;\;f(x)$ es constante (no creciente y no decreciente) para $x ∈[ 3 ,6].$



• Signo de la función:
  $\;\;\;f(x) > 0$ para $x ∈ (-\infty,0 ) ∪[ 3 ,6 ]$; los valores de $y=f(x)$ son positivos para esos valores de $x$, la gráfica está en el $1º$ y $2º$ cuadrante del sistema de ejes coordenados.
  $\;\;\;f(x) < 0$ para $x ∈ ( 0 ,3 )$; los valores de $y=f(x)$ son negativos para esos valores de $x$, la gráfica puede estar en el $3º$ y $4º$ cuadrante del sistema de ejes coordenados.



• Asíntotas horizontales: no tiene, el
  $\underset{x\to -\infty }{\lim}f(x)=\underset{x\to -\infty }{\lim} x^2-4x:\infty-\infty∶indeterminado\;\;\;$ $\underset{x\to -\infty }{\lim} x^2-4x=\underset{x\to -\infty }{\lim} x^2(1-\frac{4}{x})=\infty(1-0)=\infty$, el resultado no es una constante por lo que no hay asíntota horizontal.



• Asíntotas verticales: no tiene, ningún valor de $x$ genera una división entre cero en la función.



• Continuidad:
  $\;\;\;f(x)$ es continua en el intervalo $(-\infty ,3 )$ porque $\underset{x\to a }{\lim}\; x^2-4x=a^2-4a=f(a)$ para $a ∈(-\infty ,3 )$;
  $\;\;\;f(x)$ es discontinua en $x=3$ porque $\underset{x\to 3^-}{\lim}\;⁡x^2-4x=-3\;\;\;$ y $\;\;\;\underset{x\to 3^+}{\lim}\;⁡⁡4=4$, por lo tanto $\underset{x\to 3}{\lim}\;⁡f(x)\;\; No\; existe.$
  
  $\;\;\;f(x)$ es continua en el intervalo $[ 3 ,6 ]$ porque $\underset{x\to a }{\lim}\; 4=4=f(a)$ para $a ∈( 3 ,6 ) $ y se puede cerrar el intervalo porque $\underset{x\to 3^+}{\lim}\;⁡4=4=f(3)\;\;\;$ y $\;\;\;\underset{x\to 6^- }{\lim}⁡\;4=4=f(6).$



• Clasificación del punto de discontinuidad: $f(x)$ es discontinua esencial (de salto) en $x=3$ porque $\underset{x\to 3^-}{\lim}\;⁡x^2-4x=-3\;\;\;$ y $\;\;\;\underset{x\to 3^+}{\lim}\;⁡⁡4=4$ entonces $\underset{x\to 3}{\lim}\;⁡f(x)\;\; No\; existe.$