Función Racional
Una función racional tiene la forma $f(x)=\frac{P_n(x)}{Q_m(x)}$ donde $P_n(x)$ es una constante o un polinomio de grado $n$ y $Q_m(x)$ es otro polinomio de grado $m$.
El ejemplo básico de una función racional es la hipérbola (girada y trasladada) cociente de dos polinomios de primer grado o constante sobre polinomio de primer grado, que en su forma más simple es $f(x)=\frac{1}{x}$ cuya gráfica es:
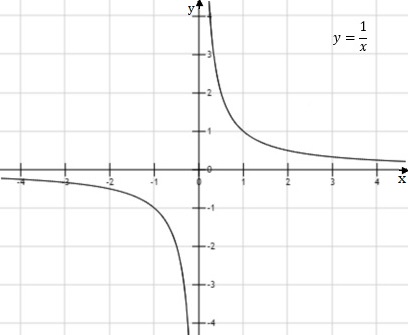
- Dominio: $D_f : \; x\in\mathbb{R}-\left \{ 0 \right \}$.
- Ceros o raíces: no tiene.
- Paridad: función impar, gráfica simétrica al origen. Satisface que $f(-x)=-f(x)$.
- Punto de corte al eje y: no tiene.
- Asíntota horizontal: $y=0$.
Límites: $\underset{x\to \infty}{\lim}\frac{1}{x}=\frac{1}{\infty}= 0$
$\underset{x\to -\infty}{\lim}\frac{1}{x}=\frac{1}{-\infty}= 0$
- Asíntota vertical: $x=0$.
Límites: $\underset{x\to 0}{\lim}\frac{1}{x}:\frac{1}{0}$
Límites laterales: $\underset{x\to 0^-}{\lim}\frac{1}{x}=\frac{1}{0^-}= -\infty \; \;$ $\underset{x\to 0^+}{\lim}\frac{1}{x}=\frac{1}{0^+}= +\infty$
$\underset{x\to 0}{\lim}\frac{1}{x}: No\; existe,\; límites\; laterales\; diferentes. $
- Intervalos de continuidad:
Función continua para $ x\in\mathbb{R}-\left \{ 0 \right \}$.
Punto de discontinuidad esencial o infinita en $x=0$.
- Rango: $ y \in\mathbb{R}-\left \{ 0 \right \}$
- Monotonía: $f(x)$ es decreciente para, $ x\in (0, \infty)$, y decreciente para $x\in (-\infty,\;0)$.
- Signos de la función:
La función es positiva, $f(x)>0$ para $x \in (0,\infty)$
La función es negativa, $f(x)<0$ para $x \in (-\infty,\;0)$
Otro Ejemplo:
Para la función $f(x)=\frac{x^3-9x}{x^3-16x}$
Obtener el dominio, los ceros o raíces, la paridad, el punto de corte al eje $y$, las asíntotas verticales y horizontales, los intervalos de continuidad y clasificación de discontinuidades, el esbozo gráfico, el rango, la monotonía y los intervalos donde es positiva o cero y donde es negativa.
- Dominio: el dominio de la función son todos los reales tales que su denominador es diferente de cero:
$x^3-16x\neq0$
$x(x^2-16)\neq0$
$x\neq0$ $x^2\neq16$
$x\neq\pm4$
$x\in\mathbb{R}-\left \{ -4,0,4 \right \}$
o $D_f=(-\infty,-4)\cup(-4,0)\cup(0,4)\cup(4,\infty)$, ya que para esos valores de $x$ se puede obtener su valor correspondiente de $y$.
- Ceros o raíces: $y=f(x)=0$
$\frac{x^3-9x}{x^3-16x}=0$
$x^3-9x=0$
$x(x^2-9)=0$
$x=0$ pero $x=0 {\notin} D_f$ entonces no es raíz
$x^2=9$
$x=\pm3$
La función tiene dos raices $x=-3$ y $x=3$.
La gráfica corta al eje $x$ en $-3$ y $3$ coordenadas $(-3,0)$ y $(3,0)$
- Paridad:$$f(-x)=\frac{(-x)^3-9(-x)}{(-x)^3-16(-x)}=\frac{-x^3+9x}{-x^3+16x}=\frac{-(x^3-9x)}{-(x^3-16x)}=\frac{x^3-9x}{x^3-16x}=f(x)$$
$f(x)$ es par, su gráfica es simétrica con respecto al eje $y$.
- Punto de corte al eje $\boldsymbol{y}$:
$y=f(0)$ pero $x=0\notin D_f, \; \;f(0)$ no existe. Por lo que no hay punto de corte al eje $y$.
- Asíntotas verticales: (calcular el límite de la función en los valores que generen una división entre cero en la función)
$$\lim_{x\rightarrow 0}\frac{x^3-9x}{x^3-16x}: \;\frac{0}{0} \; indeterminado. $$
$$\lim_{x\rightarrow 0}\frac{x(x^2-9)}{x(x^2-16)}= \lim_{x\rightarrow 0}\frac{x^2-9}{x^2-16}=\frac{-9}{-16}=\frac{9}{16}\approx0.56$$
La función no tiene asíntota vertical en $x=0$
$$\lim_{x\rightarrow 4}\frac{x^2-9}{x^2-16}: \;\frac{7}{0} \; \; ¿-\infty, \infty \; \; \text{o no existe}? $$ Hay que calcular límites laterales:
$$\lim_{x\rightarrow 4^+}\frac{x^2-9}{x^2-16}=\frac{7}{0^+}=\infty$$
$x$ se acerca a $4$ por la derecha tomando valores como $4.1$, $4.01$, $4.001$ etc. entonces el denominador se acerca a cero tomando únicamente valores positivos y el cociente de un número positivo entre un número positivo da un número positivo, por lo que el resultado del límite es infinito.
$$\lim_{x\rightarrow 4^-}\frac{x^2-9}{x^2-16}= \frac{7}{0^-}=-\infty$$ $x$ se acerca a $4$ por la izquierda tomando valores como $3.9$, $3.99$, $3.999$ etc. entonces el denominador se acerca a cero tomando únicamente valores negativos y el cociente de un número positivo entre un número negativo da un número negativo, por lo que el resultado del límite es menos infinito.
$$\lim_{x\rightarrow 4}\frac{x^2-9}{x^2-16} \; \; \; \text{ no existe}$$
No existe, ya que los 2 límites laterales son diferentes.
$f(x)$ tiene una asíntota vertical de ecuación $x=4$ y por la paridad de la función tendrá otra de ecuación $x= - 4$, la gráfica de la función es simétrica con respecto al eje $y$.
Asíntotas horizontales: (calcular el límite de la función en infinito y en menos infinito)
$$\lim_{x\rightarrow \infty}\frac{x^2-9}{x^2-16}: \;\frac{\infty}{\infty} \; \text{Indeterminado.} $$
$$\lim_{x\rightarrow \infty}\frac{x^2(1-\frac{9}{x^2})}{x^2(1-\frac{16}{x^2})}=\lim_{x\rightarrow \infty}\frac{1-\frac{9}{x^2}}{1-\frac{16}{x^2}}=\frac{1-0}{1-0}=1 $$
y análogamente
$$\lim_{x\rightarrow -\infty}\frac{x^2-9}{x^2-16}=1 $$
$f(x)$ tiene una asíntota horizontal de ecuación $y=1$.
Intervalos de continuidad: $f(x)$ es continua en su dominio ya que $$\lim_{x\rightarrow a}\frac{x^3-9x}{x^3-16x}=\frac{a^3-9a}{a^3-16a}=f(a)$$ para todo valor de $a$ diferente de $-4,$ $0$ y $4$. Por lo que $f(x)=\frac{x^3-9x}{x^3-16x}$ es continua en el intervalo $(-\infty,-4)\cup(-4,0)\cup(0,4)\cup(4,\infty)$
Clasificación de discontinuidades:
la función es discontinua removible en $x=0$ ya que tiene límite en ese punto $\lim_{x\rightarrow 0}\frac{x^3-9x}{x^3-16x}=\frac{9}{16}\approx0.56$, la gráfica presenta un agujero de coordenadas $(0 ,\frac{9}{16})$. Y es discontinua esencial infinita en $x=4$ y en $x=-4$ porque los límites en esos puntos no existen.
Esbozo gráfico:
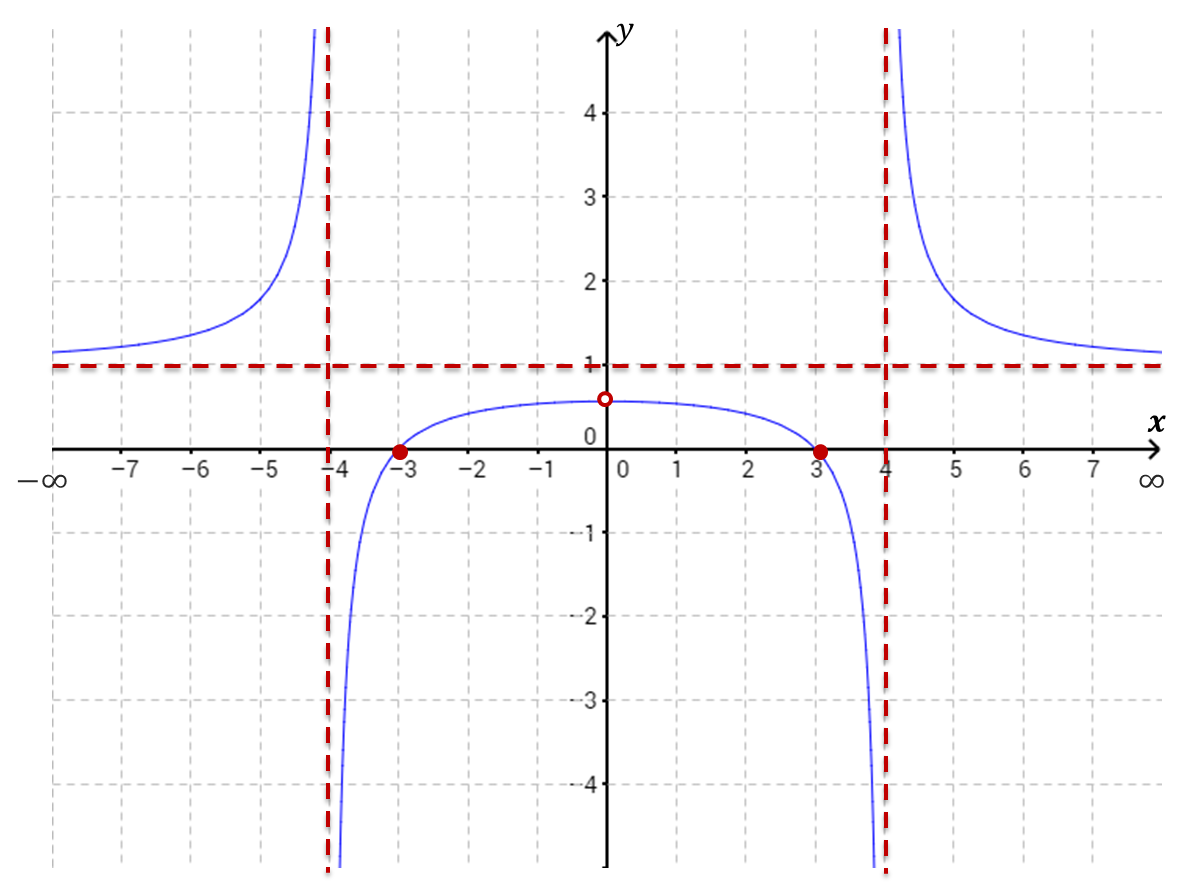 |
Rango: $y\in(-\infty,\frac{9}{16})\cup(1,\infty) $ o $R_f$=$ (-\infty,\frac{9}{16})\cup(1,\infty) $
Monotonía:
$y=f(x)$ crece para $ x\in(-\infty,-4)$ (los valores de $y$ aumentan, vistos de izquierda a derecha como lo indica el sentido positivo del eje $x$).
$y=f(x)$ crece también para $ x\in(-4,0)$.
$y=f(x)$ decrece para $ x\in(0,4)$ (los valores de $y$ disminuyen, vistos de izquierda a derecha como lo indica el sentido positivo del eje $x$).
$y=f(x)$ decrece también para $ x\in(4,\infty)$.
Intervalos donde la función es positiva o cero y donde es negativa.
De la gráfica se puede ver que
$\boldsymbol{y=f(x)\geq0:} \text{ para } x\in(-\infty,-4)\cup[-3,0)\cup(0,3]\cup(4,\infty)$
$\boldsymbol{y=f(x)<0:} \text{ para } x\in(-4,-3)\cup(3,4)$




