


Una doble desigualdad es del tipo: $a > b > c$ y es la intersección de $a>b$ y $b>c$ e implica que $a > c$ (la relación podría ser $\geq$ o también $<$ 0 $\leq$ y se tratarían de la misma manera).
Por ejemplo si $a$, $b$ y $c$ son números se podría tener que $5 > 3 > 1$, donde se ve claro que $5 > 1$ y resume a $5>3$ y $3>1$. En otro caso $-7 \leq -3 \leq1$ donde $-7\leq1$ y resume a $-7\leq-3$ y $-3\leq1$.
Cuando $a$, $b$ y $c$ son expresiones algebraicas, una doble desigualdad $a > b > c$ significa que se deben satisfacer simultáneamente las dos desigualdades $a > b$ y $b > c$ y también implica que $a>c$.
La solución de $a > b > c$ será la intersección de la soluciones de $a > b$ y $b > c$, ya que se deben satisfacer ambas desigualdades.
$3x + 2 ≥ 2 - 4x $ y $2 – 4x ≥ 5x – 3$
$3x +4x ≥ 2 - 2 $ $– 4x-5x ≥ – 3-2$
$7x ≥ 0$ $- 9x ≥ - 5$
$x ≥ 0$ $\cap $ $x ≤ \frac{5}{9}$
Gráficamente:
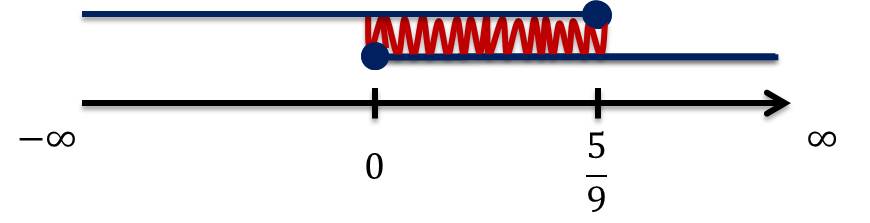
$\boldsymbol{0 ≤ x ≤ \frac{5}{9}}$
o $\boldsymbol{x\in[\;0,\frac{5}{9}\;] }$
$9-2\leq 2-4x-2 \leq12-2$
$7\leq -4x \leq10$
$\frac{7}{-4}\geq \frac{-4x}{-4} \geq\frac{10}{-4}$
$-\frac{7}{4}\geq x \geq-\frac{10}{4}$
$-\frac{5}{2}\leq x \leq-\frac{7}{4}$
Gráficamente:
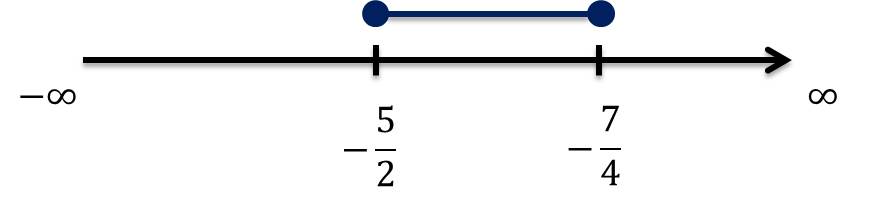
$\boldsymbol{x\in[-\frac{5}{2},-\frac{7}{4}] }$
$2x-1 < x-2 $ y $x-2\leq-x^2$
$2x-x < -2+1 $ $x^2+x-2\leq0$ (Se resulve la desigualdad cuadrática)
$x < -1$ $\cap $ $-2\leq x\leq1$ (Solución de la desigualdad cuadrática)
Gráficamente:
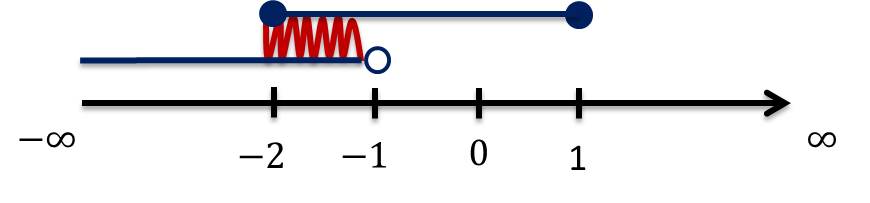
$\boldsymbol{-2≤ x< -1}$ o $\boldsymbol{x\in[-2,-1)} $