• Tu propones el ejercicio
• Nosotros te proponemos el ejercicio

Función polinomial

Un polinomio es una función que tiene la forma:  $$f(x)=a_n x^n + a_{n-1} x^{n-1}+...+a_2 x^{2}+a_1 x+ a_0$$

donde $a_i$ son constantes reales y $n$ es un entero positivo.

De manera general ya se puede decir que:

1. Tienen dominio $D_f=(\;-\infty,\;\infty)$, a menos que se indique explícitamente otro.


2. Un polinomio de grado n tiene n raíces reales y/o complejas, y puede factorizarse en términos de ellas.

   Factorización: La factorización de un polinomio en $x$ de grado $n$, $P_n(x)=a_{n}x^n+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}$,  en términos de sus  $n$  raíces (reales y/o complejas),  $r_1, r_2, ... r_n$,  es su expresión como el producto del coeficiente del término de grado  $n:a_n$,  multiplicado por los  $n$  factores de la forma:  $x$  menos la raíz (para cada una de las raíces reales y/o complejas), $P_n (x)=a_n(x-r_1)(x-r_2)...(x-r_n)$.

   La multiplicidad de una raíz, es decir, el número de veces que cuenta como raíz de una función polinomial, es igual al número de factores lineales iguales en la factorización del polinomio, correspondientes a esa raíz.

   Cuando no se conocen todas las raíces o únicamente interesa factorizar en términos de las raíces reales, se puede hacer una factorización parcial como $P_n (x)=(x-r_1)Q_{n-1} (x)$...(1).

   Donde $Q_{n-1}(x)$ es otro polinomio de grado $n-1$ , que se obtiene al dividir $P_n (x)$ entre $x-r_1$ , como puede verse de (1). Este proceso puede repetirse buscando ahora las raíces de $Q_{n-1}$ y continuar hasta donde sea posible.

3. Son funciones continuas en todo su dominio porque: $$\lim_{x\rightarrow c}\;a_nx^n+a_{n-1}x^{n-1}+...+a_2x^2+a_1x+a_0=$$ $$a_nc^n+a_{n-1}c^{n-1}+...+a_2c^2+a_1c+a_0\;=f(c)$$ para $c∈D_f$


4. No tienen asíntotas verticales ya que ningún valor de $x$ genera una división entre cero.


5. No tienen asíntotas horinzontales, los límites de un polinomio cuando $x$ tiende a infinito o a menos infinito son también infinitos (positivos y/o negativos).


Los polinomios de primer grado: $f(x)=a_1x+a_0$ tienen como gráfica una recta con pendiente $a_1$ y corte al eje $y$ en $a_0$.

Los polinomios de segundo grado:$f(x)=a_2x^2+a_1x+a_0$ tiene como gráfica una párabola (con eje de simetría vertical) que:
1. tienen ceros o raíces (puntos de corte al eje $x$) en $x_{1,2}=\frac{-a_1±\sqrt{{a_1}^2-4a_2a_0}}{2a_2}$ o no, si ${a_1}^2-4a_2a_0 <0$,


2. corte al eje $y$ en $a_0$


3. tiene vértice en $(x_v, y_v)$ donde $x_v=\frac{-a_1}{2a_2} $ y $y_v=f(x_v)$;


4. abre hacia arriba si $a_2>0$ y abre hacia abajo si $a_2<0$ (ver desigualdades de segundo grado)



Ejemplo:

Para la función  $f(x)=2x^3-8x$  (polinomio de tercer grado con $a_3=2$, $a_2=0$, $a_1=-8$,  y  $a_0=0$).



Obtener el dominio, los ceros o raíces, la paridad, el punto de corte al eje  $y$,  las asíntotas verticales y horizontales, los intervalos de continuidad y clasificación de discontinuidades, el esbozo gráfico, el rango, la monotonía y los intervalos donde es positiva o cero y donde es negativa.
• Dominio: el dominio de la función son todos los reales,  $x\in\mathbb{R}$  o  $D_f=(-\infty,\infty)$, ya que para todo valor de $x$ en los reales se puede obtener su valor correspondiente de $y$ .


• Ceros o raíces: $y=f(x)=0$;
  
                                                  $2x^3-8x=0$
                                                $2x(x^2-4)=0$
                                                  $x=0$    $x^2=4$
                                                                $x=\pm2$
  
  Las raices de la fución son: $x=-2$,  $x=0$  y  $x=2$.


• Paridad: $f(-x)=2(-x)^3-8(-x)$
                           $=-2x^3+8x$
                           $=-(2x^3-8x)$
                           $=-f(x)$

  $f(x)$ es impar, su gráfica es simétrica con respecto al origen.



• Punto de corte al eje $\boldsymbol{y}$:
  $y=f(0)=2(0)^3-8(0)=0$  el punto tiene coordenadas  (0,0)  que es el origen.


• Asíntotas verticales: no tiene, ya que ningún valor de $x$ genera una división entre cero en la función.


• Asíntotas horizontales: $$\lim_{x\rightarrow \infty} 2x^3-8x: \;\infty -\infty: indeterminado$$ $$\lim_{x\rightarrow \infty} x^3(2-\frac{8}{x^2})=\infty(2-0)=\infty\;\;\;\;\;\;\;\;\;\;$$ $$\lim_{x\rightarrow -\infty} x^3(2-\frac{8}{x^2})=-\infty(2-0)=-\infty\;\;\;\;$$

  $f(x)$ no tiene asíntotas horizontales.



• Intervalos de continuidad: $f(x)$ es continua en todos los reales ya que   $$\lim_{x\rightarrow a} 2x^3-8x=2a^3-8a=f(a)$$  para todo valor de $a$ en los números reales.


• Clasificación de discontinuidades: la función no tiene puntos de discontinuidad.


• Esbozo gráfico

  Tomando en cuenta todos los resultados anteriores y tabulando un par de puntos:

            $f(-1)=2(-1)^3-8(-1)=6$, $f(1)=2(1)^3-8(1)=-6$ .



• Rango: $y\in\mathbb{R}$  o  $R_f$ $=(-\infty,\infty)$,


• Monotonía: $y=f(x)$ crece para  $x\in(-\infty,x_2]$  (los valores de $y$ aumentan, vistos de izquierda a derecha como lo indica el sentido positivo del eje $x$). Le llamamos  $x_1$ y $x_2$,  a los valores de  $x$  donde la curva da vuelta porque todavía no los podemos calcular analíticamete.

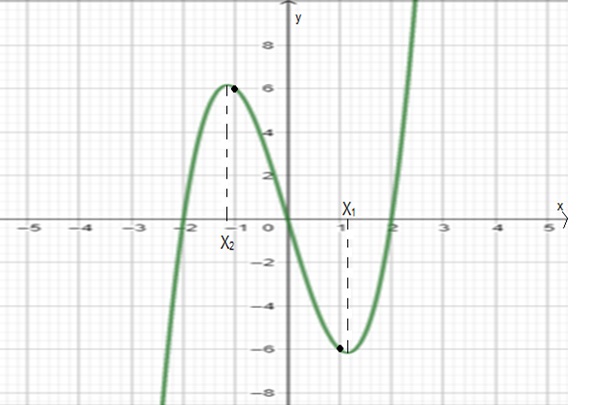  y=f(x)  decrece para  $x\in[x_2,x_1]$  (los valores de $y$ disminuyen, vistos de izquierda a derecha como lo indica el sentido positivo del eje x).

  $y=f(x)$ crece para  $x\in[x_1,\infty)$



• Intervalos donde la función es positiva o cero y donde es negativa.
  
  De la gráfica se puede ver que
  
  $\boldsymbol{y=f(x)\geq0:}$ para $x\in[-2,0]\cup[2,\infty)$

$\boldsymbol{y=f(x) < 0:}$ para $x\in(-\infty,-2) \cup (0,2)$