1. Resolver las siguientes desigualdades:
a) $-3x^2+5\geq-x+1$
Pasando todos los términos de lado derecho de la desigualdad se obtiene
$0\geq3x^2-x+1-5$
$0\geq3x^2-x-4$
Se factoriza el lado derecho de la desigualdad para obtener
$0\geq(3x-4)(x+1)$
La solución de la desigualdad corresponde a la unión de las soluciones de los siguientes casos:
Caso i) Un término mayor o igual a cero y el otro menor o igual a cero
$3x-4\geq0\rightarrow x\geq \frac{4}{3}$ y $x+1\leq0\rightarrow x\leq-1$
$ Sol= \varnothing$
Caso ii) Los términos con el signo contrario al caso anterior
$3x-4\leq0\rightarrow x\leq \frac{4}{3}$ y $x+1\geq0\rightarrow x\geq-1$
$ Sol= \left[-1,\frac{4}{3}\right]$
Por lo tanto, la solución total de la desigualdad es el intervalo $\left[-1,\frac{4}{3}\right]$
b) $\frac{5-3x}{4x-2}\leq2$
Pasando todos los términos de lado derecho de la desigualdad se obtiene
$0\leq2-\frac{5-3x}{4x-2}\rightarrow0\leq2+\frac{3x-5}{4x-2}\rightarrow0\leq\frac{11x-9}{4x-2}$
La solución de la desigualdad corresponde a la unión de las soluciones de los siguientes casos:
Caso i) El numerador del cociente en la desigualdad mayor o igual a cero y el denominador positivo
$\left(11x - 9 \geq 0 \rightarrow x \geq \frac{9}{11}\right)$ y $\left(4x - 2 > 0 \rightarrow x > \frac{1}{2}\right)$
$ Sol= \left[\frac{9}{11},\infty\right)$
Caso ii) El numerador del cociente en la desigualdad menor o igual a cero y el denominador negativo
$\left(11x - 9 \leq 0 \rightarrow x \leq \frac{9}{11}\right)$ y $\left(4x - 2 < 0 \rightarrow x < \frac{1}{2}\right)$
$ Sol= \left(\infty,\frac{1}{2}\right]$
Por lo tanto, la solución total de la desigualdad es el intervalo
$\left(\infty,\frac{1}{2}\right] \cup \left[\frac{9}{11},\infty\right)$
2. Considerar las funciones
$f(x) = \sqrt{x-1}$ y $g(x)=\frac{2x+3}{2x^2-2}$
a) Determinar el dominio y las raíces (ceros) de cada función
El dominio de f son aquellos valores de x para los que la raíz cuadrada es mayor o igual a cero
$Dom\ (f) = \left\{ x\mathbb{\in R:}x - 1 \geq 0 \right\} = x \geq 1 = \lbrack 1,\infty)$
Las raíces de f son aquellos valores de x para los que f(x) = 0
$\left(\sqrt{x - 1} = 0\ \rightarrow \ x - 1 = 0\ \rightarrow \ x = 1\right)$
$\therefore\ Raíces(f) = \left\{ 1 \right\}$
El dominio de g son aquellos valores de x para los que el denominador de la función es diferente de cero
$2x^{2} - 2 \neq 0\ \rightarrow \ x^{2} \neq 1\ \rightarrow \ x \neq \pm 1]$
$Dom\ (g) = \left\{ x\mathbb{\in R:}2x^{2} - 2 \neq 0 \right\}\mathbb{= R - \{ \pm}1\}$
Las raíces de g son aquellos valores de x para los que g(x) = 0. Como el denominador debe ser diferente de cero, entonces el numerador se iguala a cero
$2x + 3 = 0\ \rightarrow \ x = - \frac{3}{2}$
Raíces $(g) = \{ -\frac{3}{2}\}$
b.1) Determinar las fórmulas y dominio de $\left( \frac{f}{g} \right)\left( x \right)$ y $\left( g\circ f \right)\left( \mathbf{x} \right)$
$\left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)} = \frac{\sqrt{x - 1}}{\frac{2x + 3}{2x^{2} - 2}} = \frac{\left( 2x^{2} - 2 \right)\sqrt{x - 1}}{2x + 3}$
El dominio de $\frac{f}{g}$ es la intersección del dominio de $f$ y $g$, , excepto los valores de $x$ para los que $g(x)=0$
$Dom\left( \frac{f}{g} \right) = Dom(f) \cap Dom(g) - \left\{ x\mathbb{\in R:}g(x) = 0 \right\}$
$Dom\left( \frac{f}{g} \right) = \left\lbrack \left\lbrack 1,\left. \ \infty \right) \cap \left( \mathbb{R -}\left\{ \pm 1 \right\} \right) \right.\ \right\rbrack - \left\{ - \frac{3}{2} \right\}$
$Dom\left( \frac{f}{g} \right) = (1,\infty) - \left\{ - \frac{3}{2} \right\} = (1,\infty)$
b.2) Determinar las fórmulas y dominio de $\left( g\circ f \right)\left( \mathbf{x} \right)$
$(g\circ f)(x) = g\left( f(x) \right) = g\left( \sqrt{x - 1} \right) = \frac{2\sqrt{x - 1} + 3}{2\left( \sqrt{x - 1} \right)^{2} - 2} = \frac{2\sqrt{x - 1} + 3}{2x - 4}$
El dominio de la composición son los valores de $f(x)$ que pertenecen al dominio de $g(x)$
$Dom(g\circ f) = \left\{ x \in Df:f(x) \in Dg \right\}$
$Dom(g\circ f) = \left\{ x \in \lbrack 1,\infty):\sqrt{x - 1}\mathbb{\in R - \{ \pm}1\} \right\}$
$Dom(g\circ f) = \left\{ x \in \lbrack 1,\infty):x \neq 2 \right\} = \lbrack 1,\infty) - \{ 2\}$
3. Un recipiente cilíndrico con tapa tiene una altura igual al doble de su radio.
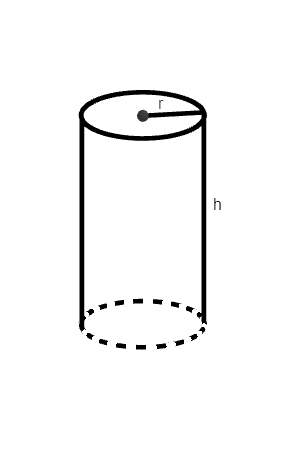
$h = 2r \rightarrow r = \frac{h}{2}$
a) Expresar el área del recipiente en función de su altura $h$
Área recipiente = Área base + Área cilindro + Área Tapa
$= \pi r^{2} + h2\pi r + \pi r^{2} = 2\pi r^{2} + h\pi 2r$
$= 2\pi\left( \frac{h}{2} \right)^{2} + h\pi h$
$= \frac{1}{2}\pi h^{2} + \pi h^{2}$
$\therefore A(h) = \frac{3}{2}\pi h^{2}$
b) Expresar el volumen del recipiente en función de su radio $r$
Volumen del recipiente = Área de la base * Altura
$= \left( \pi r^{2} \right)h = \left( \pi r^{2} \right)(2r)$
$\therefore V(r) = 2\pi r^{3}$
4. Calcular los siguientes límites:
a) $\underset{x\mathbf{ \rightarrow 0}}{\mathbf{\lim}}\frac{\mathbf{sen}\left( \mathbf{4}x \right)\mathbf{- 4}x}{\mathbf{2}x}$
${= \lim_{x \rightarrow 0}}{\frac{sen(4x)}{2x} - \lim_{x \rightarrow 0}\frac{4x}{2x}}$
$= 2\lim_{x \rightarrow 0}{\frac{sen(4x)}{4x} - \lim_{x \rightarrow 0}2} = 2(1) - 2 = 0$
b) $\underset{\mathbf{u \rightarrow 9}}{\mathbf{\lim}}\frac{\sqrt{\mathbf{u - 6}}\mathbf{\ - \ }\sqrt{\mathbf{3}}}{\mathbf{u - 9}}$
$= \lim_{u \rightarrow 9}\frac{\left( \sqrt{u - 6} - \sqrt{3} \right)\left( \sqrt{u - 6} + \sqrt{3} \right)}{(u - 9)\left( \sqrt{u - 6} + \sqrt{3} \right)}$
$= \lim_{u \rightarrow 9}\frac{(u - 6 - 3)}{(u - 9)\left( \sqrt{u - 6} + \sqrt{3} \right)}$
$= \lim_{u \rightarrow 9}\frac{u - 9}{(u - 9)\left( \sqrt{u - 6} + \sqrt{3} \right)}$
$= \frac{1}{\sqrt{3} + \sqrt{3}} = \frac{1}{2\sqrt{3}}$
c) $\underset{x\mathbf{\rightarrow \infty}}{\mathbf{\lim}}\left( x-\sqrt{x^2+x-1}\right)$
$= \lim_{x \rightarrow \infty}\frac{\left( x - \sqrt{x^{2} + x - 1} \right)\left( x + \sqrt{x^{2} + x - 1} \right)}{\left( x + \sqrt{x^{2} + x - 1} \right)}$
$= \lim_{x \rightarrow \infty}\frac{x^{2} - \left( x^{2} + x - 1 \right)}{x + \sqrt{x^{2} + x - 1}}$
$= \lim_{x \rightarrow \infty}{\frac{- x + 1}{x + \sqrt{x^{2} + x - 1}} =}$
$= \lim_{x \rightarrow \infty}\frac{- \frac{x}{x} + \frac{1}{x}}{\frac{x}{x} + \frac{1}{x}\sqrt{x^{2} + x - 1}}$
$= \lim_{x \rightarrow \infty}{\frac{- 1 + \frac{1}{x}}{1 + \sqrt{1 + \frac{1}{x} - \frac{1}{x^{2}}}} =}$
$\frac{- 1}{1 + \sqrt{1}} = - \frac{1}{2}$
5.- En el intervalo $[-\pi,\pi]$ realizar un bosquejo gráfico de la función $f(x)=2\mathbf{sen}(2x-\pi)-2$. Describiendo el orden y el tipo de operaciones gráficas utilizadas.
$\mathbf{sen}(x)$ en el intervalo $[\pi,\pi]$
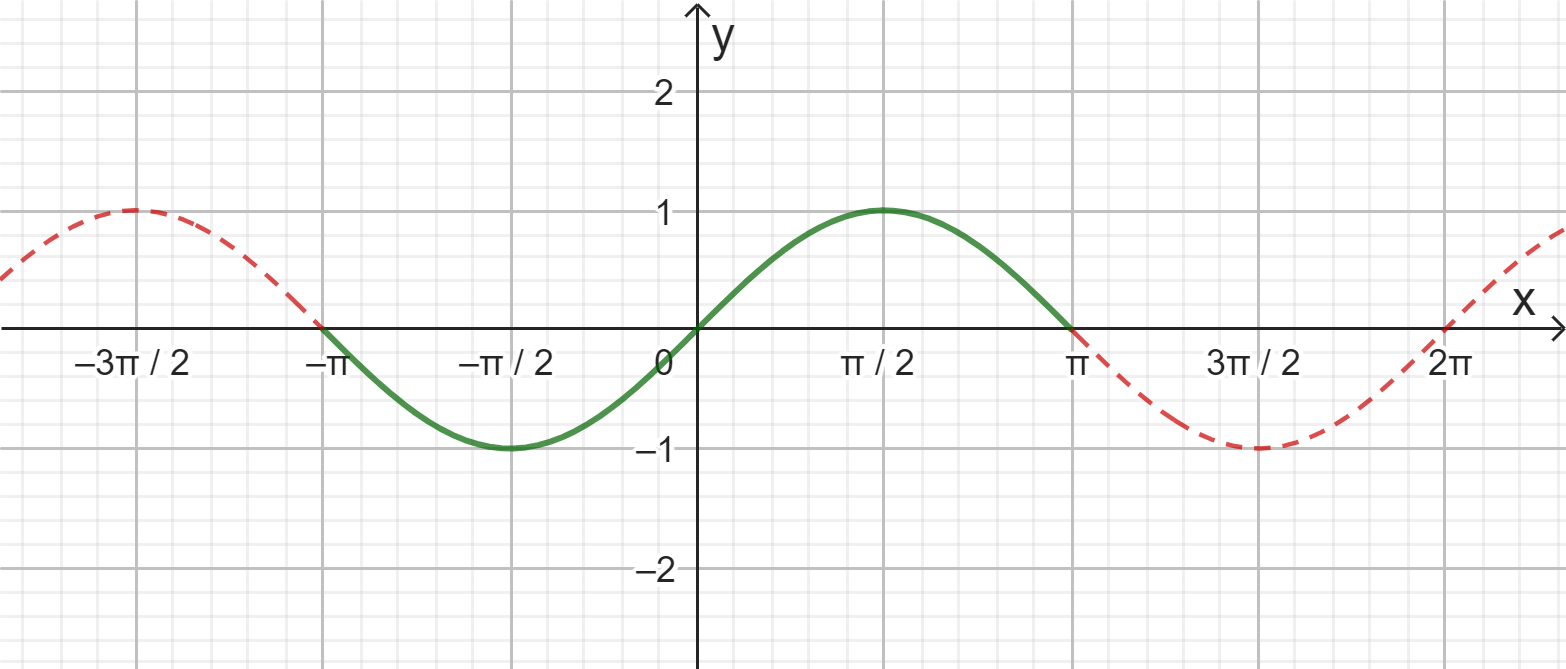
Se resta $\frac{\pi}{2}$ del argumento $(x)$ para establecer un desplazamiento horizontal a la derecha en la gráfica. Después, se multiplica el argumento por 2, lo que corresponde a una compresión horizontal.
$sen\left(2\left(\frac{x-\pi}{2}\right)\right)=sen(2x-\pi)$ en el intervalo $[-\pi,\pi]$
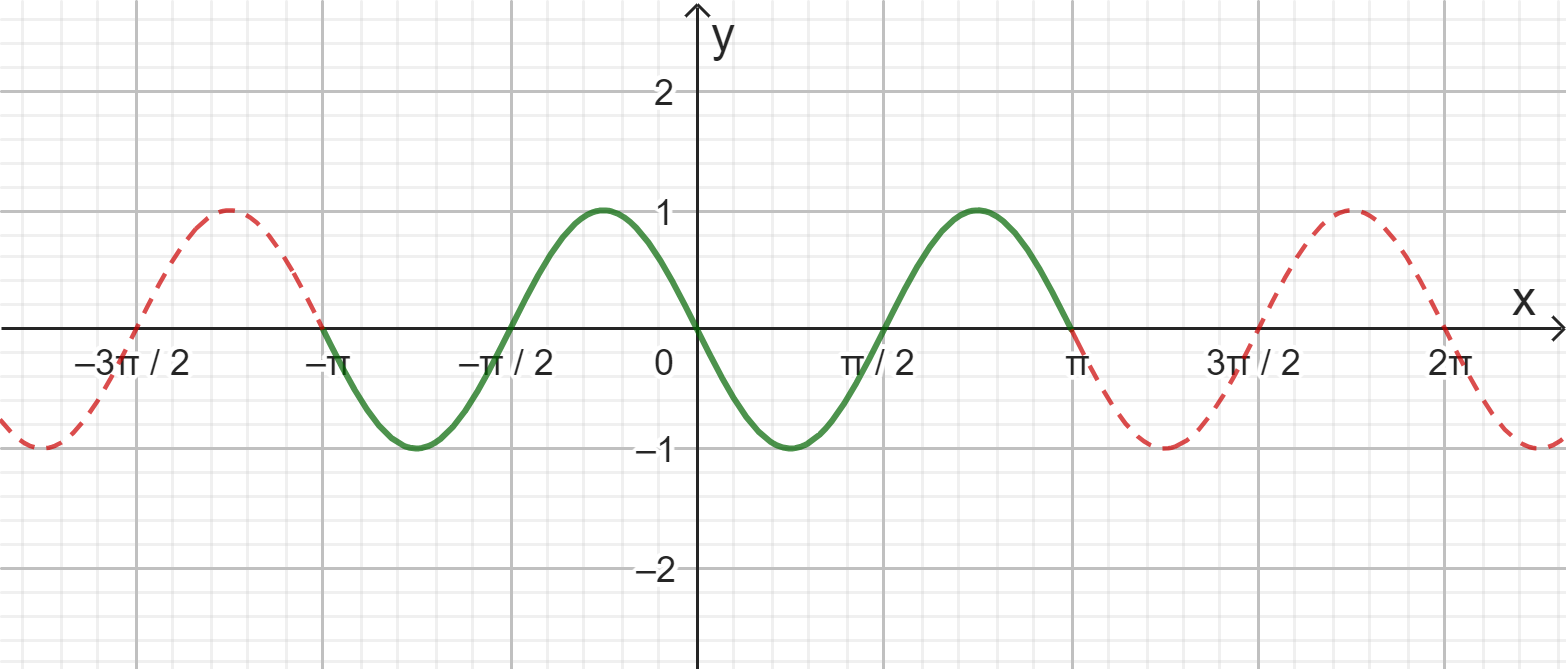
Se multiplica la función por 2 para establecer una elongación vertical. Por último, se resta 2 a la función, con lo que se su grafica se desplaza verticalmente hacia abajo. La función y gráfica finales son las siguientes:
$f(x)=2sen(2x-\pi)-2 $ en el intervalo $[-\pi,\pi]$
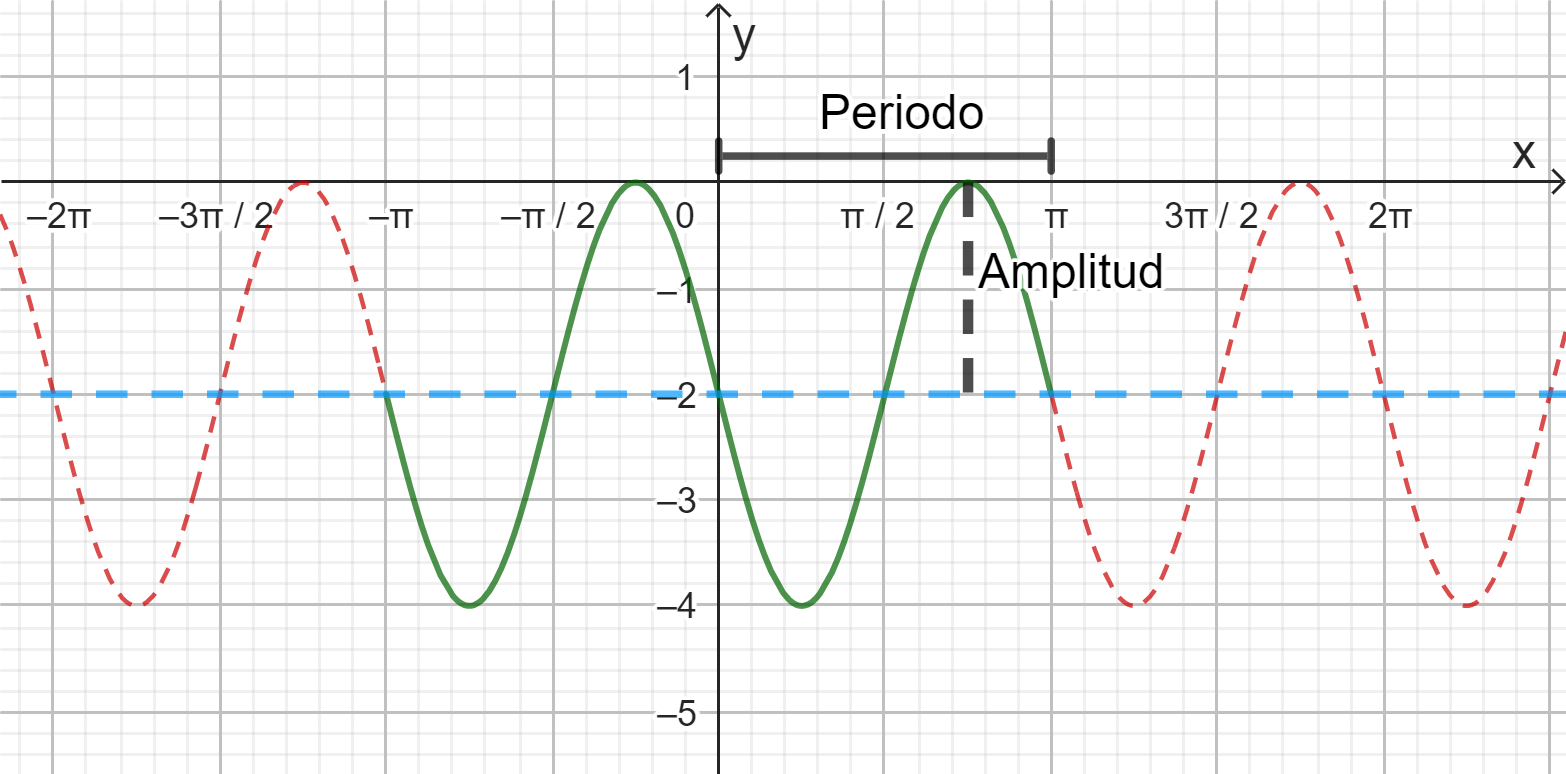
Obtener el rango, amplitud y periodo de $f(x)$.
Rango: Los valores en el eje y para los cuales $f(x)$ está definida
Rango$=[-4,0]$
Raíces: Valores de x para los que $f(x)=0$ en el intervalo $[-\pi,\pi]$. Donde la gráfica toca al eje x
Raices:$x=-\frac{\pi}{4}$ y $x=\frac{3\pi}{4}$
Amplitud: La distancia vertical desde la línea horizontal que divide a la función a la mitad hasta el punto más alto o bajo de la función.
Amplitud $= 2$
Periodo: La distancia en la que la función vuelve a tomar un mismo valor, por ejemplo f(0)=-2 y f(π)=-2.
Periodo = $\pi$
6. Sea la función $f(x) = \frac{2x^{2} - 9x + 10}{x^{2} + x - 6}$. Obtener
a) Dominio, raíces (o ceros), paridad y punto de corte con el eje y.
$f(x) = \frac{2x^{2} - 9x + 10}{x^{2} + x - 6} = \frac{(2x - 5)(x - 2)}{(x + 3)(x - 2)}$
Dominio: valores de x con los que el denominador de la función es diferente de cero
$Dom(f)=\mathbb{R}-{-3,2}$
Raíces: valores de x para los que $f(x) = 0$. El denominador no puede ser cero, por lo tanto
$(2x-5)(x-2)=0$
2 no es parte del dominio de la función, entonces
$2x-5=0$
$Raíz:x=\frac{5}{2}$
Paridad: $f(2)$ no está definida y $f(-2)=-9$, por lo tanto, la función no tiene paridad.
El punto de corte con el eje $y$ se obtiene evaluando la función en $x=0$
$f(0) = - \frac{5}{3}$
b) Ecuaciones de la asíntotas horizontales y verticales
Para determinar si la función tiene asíntotas horizontales, se calcula el límite de la función cuando x tiende a más y menos infinito
${\lim_{x \rightarrow - \infty}f(x) =}\frac{2x^{2} - 9x + 10}{x^{2} + x - 6}$
$= \lim_{x \rightarrow - \infty}f(x) = \frac{\left( 2x^{2} - 9x + 10 \right)\frac{1}{x^{2}}}{\left( x^{2} + x - 6 \right)\frac{1}{x^{2}}}$
${\lim_{x \rightarrow - \infty}f(x) =}{\frac{2 - \frac{9}{x} + \frac{10}{x^{2}}}{1 + \frac{1}{x} - \frac{6}{x^{2}}} = 2}$
Análogamente $\lim_{x \rightarrow \infty}f(x) = 2$
$\therefore y = 2$ es una asíntota horizontal
Como la función no está definida en $x=-3$ y $x=2$, se calcula el límite cuando x tiende a estos valores para determinar si la función tiene asíntotas verticales o si tiene alguna discontinuidad removible.
Primero se calcula el límite de la función cuando $x$ tiende, por la derecha y por la izquierda, a $-3$.
$f(x) = \frac{(2x - 5)(x - 2)}{(x + 3)(x - 2)} = \frac{2x - 5}{x + 3}$
Al acercarnos a $-3$ por la izquierda con valores como $-3.1$ por ejemplo, el resultado del denominador $x+3$ es negativo y cada vez más pequeño en magnitud, por lo tanto
$\lim_{x \rightarrow {- 3}^{-}}\frac{2x - 5}{x + 3} = \infty$
$\lim_{x \rightarrow {- 3}^{+}}\frac{2x - 5}{x + 3} = - \infty$
$\therefore x = - 3$ es una asíntota vertical
c) Bosquejo gráfico
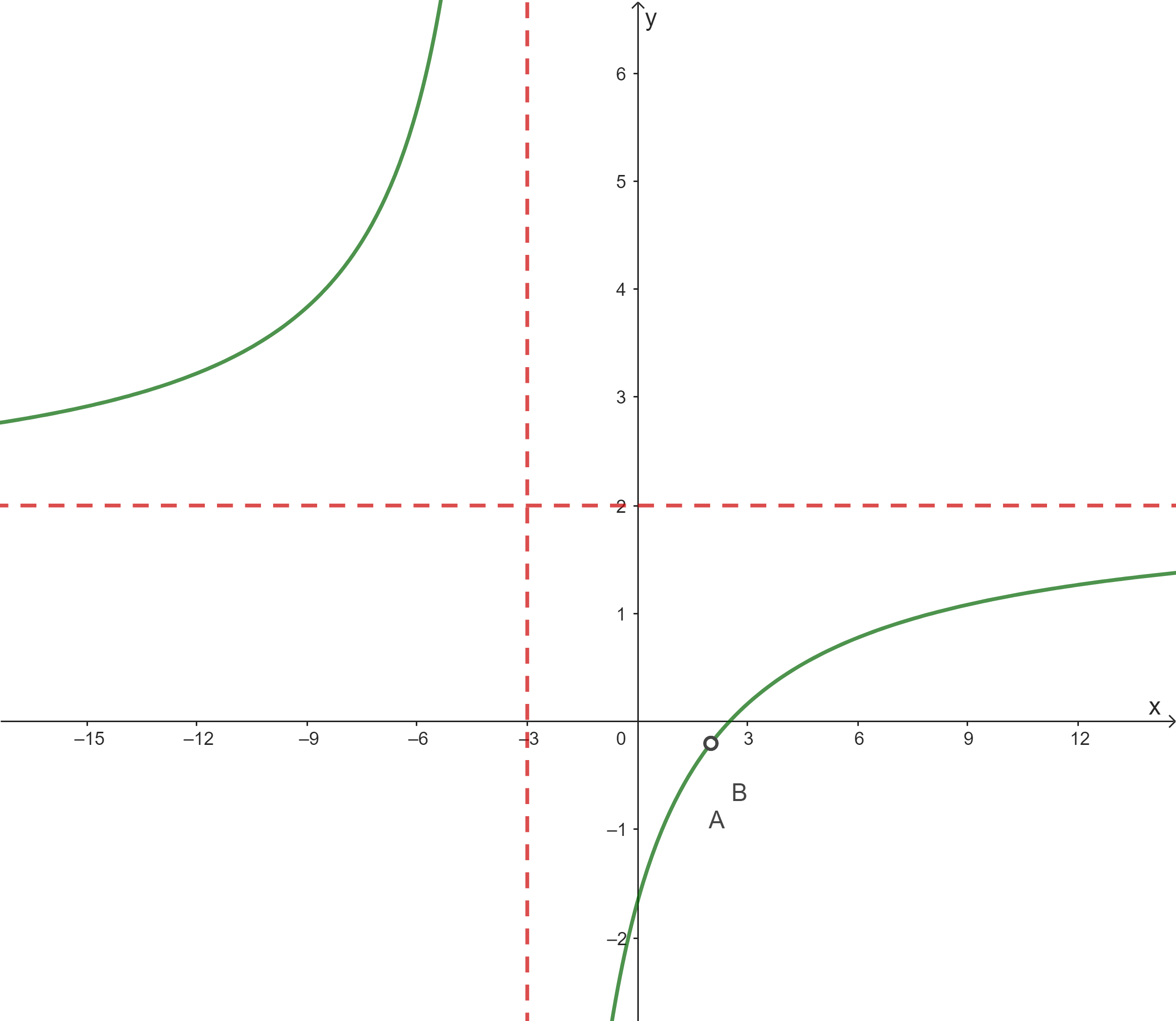
d) Intervalos de continuidad y clasificar los tipos de discontinuidades
En $x=-3$ se determinó una discontinuidad infinita.
Ahora se calcula el límite de la función cuando $x$ tiende a 2
$\lim_{x \rightarrow 2}\frac{(2x - 5)(x - 2)}{(x + 3)(x - 2)} = \lim_{x \rightarrow 2}\frac{2x - 5}{x + 3} = - \frac{1}{5}$
$\therefore$ El punto $\left( 2, - \frac{1}{5} \right)$ es una discontinuidad removible.
Los intervalos de continuidad son entonces $( - \infty, - 3) \cup ( - 3,2) \cup (2,\infty)$
e) Rango (o imagen), monotonía y para qué valores de $x, f(x)\geq0$.
A partir de la gráfica se observa que los intervalos del rango son $\left( - \infty, - \frac{1}{5} \right) \cup \left( - \frac{1}{5},2 \right) \cup \left(2,\infty\right)$
A partir de la gráfica se observa que los intervalos de monotonía son
Creciente: $\left(( - \infty, - 3) \cup ( - 3,2) \cup (2,\infty)\right)$
Los intervalos en los que la función es positiva, es decir, en los que su gráfica está encima del eje $x$ son $f \geq 0$ en $( - \infty, - 3) \cup \left( \frac{5}{2},\infty \right)$
7. Determinar los valores de las constantes $a$ y $b$ para que la siguiente función sea continua en todo su dominio
$f(x)\left\{ \begin{matrix} 3 - ax^{2}\ \ \ si\ x < - 3 \\ 2 - 3b\ \ \ \ \ si\ x = - 3 \\ 10x - 1\ \ si\ x > - 3 \\ \end{matrix} \right.$
Para que $f$ sea continua se debe cumplir
$\lim_{x \rightarrow {- 3}^{-}}f(x) = \lim_{x \rightarrow {- 3}^{+}}f(x)$ y $\lim_{x \rightarrow - 3}f(x) = f( - 3)$
Entonces, calculando los respectivos límites se obtiene
$\lim_{x \rightarrow {- 3}^{-}}3 - ax^{2} = 3 - 9a$ y $\lim_{x \rightarrow {- 3}^{+}}10x - 1 = - 31$
Se igualan ambos resultados para obtener el valor de $a$
$3 - 9a = - 31 \rightarrow a = \frac{34}{9}$
Ahora se considera la parte de la función en $x=-3$ para obtener el valor de $b$
$f( - 3) = 2 - 3b$
$- 31 = 2 - 3b \rightarrow b = 11$
Por lo tanto, $a = \frac{34}{9}$ y $b = 11$ hacen a $f$ continua en todo su dominio.
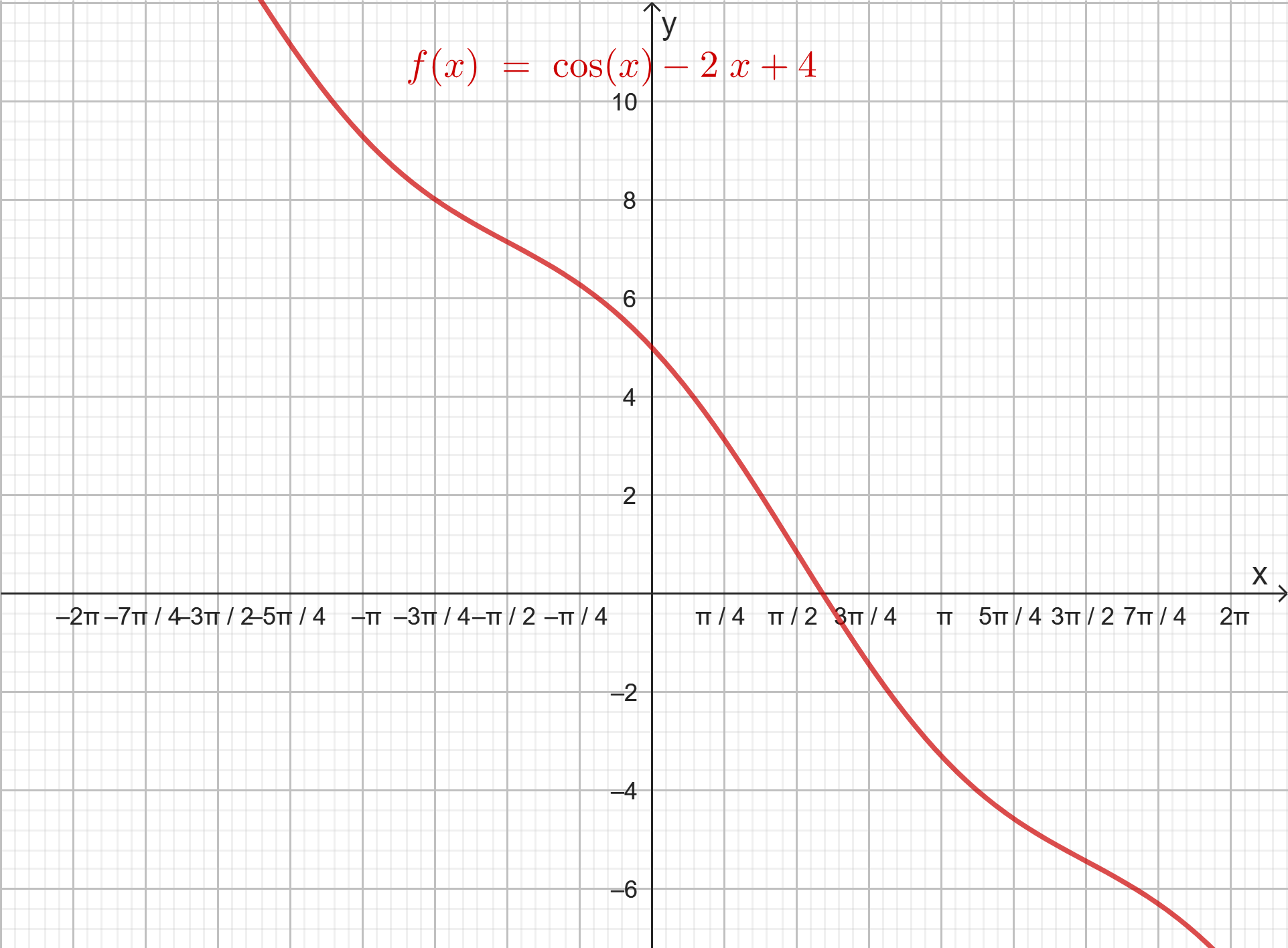
8.- Encontrar un intervalo de longitud $\frac{\pi}{4}$ o menor, que contenga una solución de la ecuación $cos(x)-2x+4=0$. Justifique su respuesta utilizando el teorema del valor intermedio.
Considerando $f(x)=cos(x)-2x+4$
Aplicando el teorema de valor intermedio se obtiene
$f\left( \frac{\pi}{2} \right) = \cos\left( \frac{\pi}{2} \right) - 2\frac{\pi}{2} + 4 = 0 - \pi + 4 > 0$
$f\left( \frac{3\pi}{4} \right) = \cos\left( \frac{3\pi}{4} \right) - 2\left( \frac{3\pi}{4} \right) + 4 = - \frac{1}{12} - \frac{3\pi}{2} + 4 < 0$
$\therefore$ En el intervalo $\left\lbrack \frac{\pi}{2},\frac{3\pi}{4} \right\rbrack$ existe una raíz de la ecuación