


1. Resolver las siguientes desigualdades:
a) $10x^2 + x - 3 \le 0$
Primero
\begin{align*}
10x^{2}+x-3\leq 0 \Rightarrow (5x+3)(2x-1)\leq 0.
\end{align*}
Tenemos que analizar dos casos.
Caso 1:
\begin{align*}
\begin{matrix}
5x+3\leq 0 & \& & 2x-1\geq 0 \\
x\leq -\dfrac{3}{5} & \& & x\geq \dfrac{1}{2} \\
& CS_{1}=\varnothing &
\end{matrix}
\end{align*}
Caso 2:
\begin{align*}
\begin{matrix}
5x+3\geq 0 & \& & 2x-1\leq 0 \\
x\geq -\dfrac{3}{5} & \& & x\leq \dfrac{1}{2} \\
& CS_{2}=\left[-\dfrac{3}{5}, \dfrac{1}{2} \right] &
\end{matrix}
\end{align*}
Por lo tanto, el conjunto solución de la desigualdad original es
\begin{align*}
CS=CS_{1} \bigcup CS_{2}= \varnothing \bigcup \left[-\dfrac{3}{5}, \dfrac{1}{2} \right]=\left[-\dfrac{3}{5}, \dfrac{1}{2} \right].
\end{align*}
b) $\displaystyle \frac{2x + 3}{x - 1} > 1$
Primero obtenemos una desigualdad equivalente:
\begin{align*}
\dfrac{2x+3}{x-1}>1 \Leftrightarrow \dfrac{2x+3}{x-1}-1>0 \Leftrightarrow \frac{x+4}{x-1}>0.
\end{align*}
Para resolver la última desigualdad, debemos que analizar dos casos.
Caso 1:
\begin{align*}
\begin{matrix}
x+4<0 & \& & x-1<0 \\
x<-4 & \& & x<1 \\
& CS_{1}=\left( -\infty, -4 \right) &
\end{matrix}
\end{align*}
Caso 2:
\begin{align*}
\begin{matrix}
x+4>0 & \& & x-1>0 \\
x>-4 & \& & x>1 \\
& CS_{2}=\left( 1,+\infty \right) &
\end{matrix}
\end{align*}
Por lo tanto, el conjunto solución de la desigualdad original es
\begin{align*}
CS=CS_{1} \bigcup CS_{2}= \left( -\infty, -4 \right) \bigcup \left( 1,+\infty \right)=\mathbb{R}-[-4,1].
\end{align*}
2. Sea la función $f (x)$ definida por:
\[f(x) =
\begin{cases}
|x + 6| - 1, & \text{si } -10 < x < -3,\\[6pt]
-\frac{x}{2} + 1, & \text{si } -3 \le x \le 3,\\[6pt]
(x - 7)^2 + 1, & \text{si } x > 3
\end{cases}
\]
a) Elaborar el bosquejo de la gráfica de $f(x)$.
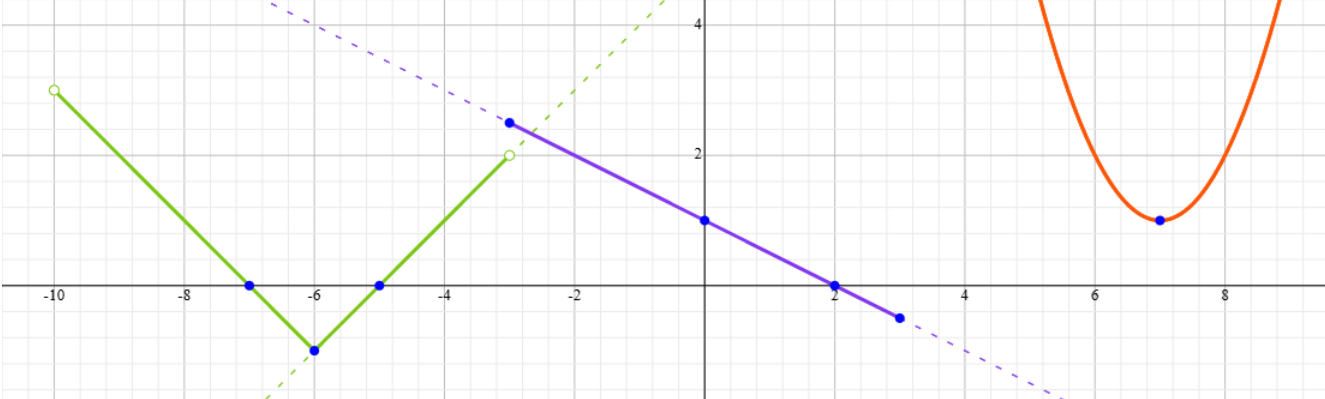
b) Determinar el dominio y las raíces.
De la gráfica de $f$ identificamos que las raíces son: $r_{1}=-7$, $r_{2}=-5$ y $r_{3}=2$.
De la regla de correspondencia de $f$, tenemos que su dominio es
\begin{align*}
D_{f}=\left(-10, -3\right) \cup [-3,3] \cup \left( 3, +\infty \right)=\left(-10, +\infty \right).
\end{align*}
c) Determinar la paridad, la monotonía y el rango.
La función no es par ni es impar.
La función es creciente en: $[-6,-3]$ y $[7,+\infty)$.
La función es decreciente en: $(-10,-6]$, $[-3,3]$ y $(3,7]$.
d) Determinar los intervalos donde $f(x) > 0$ y donde $f(x) < 0$.
La función es $f(x)>0$ en: $(-10,-7) \cup (-5,2) \cup (3,+\infty)$.
La función es $f(x)<0$ en: $(-7,-5) \cup (2,3)$.
3. Considerar las siguientes funciones:
\[
f(x) = \sqrt{x - 5}
\quad\text{y}\quad
g(x) = \frac{x - 1}{x}.
\]
a) Determinar el dominio y las raíces de cada función.
En el caso de $f$, el radicando tiene que ser positivo. Esto es,
\begin{align*}x-5\geq 0 \Rightarrow x\geq 5.\end{align*}
Por lo tanto, $D_{f}=[5,+\infty)$.
Para el caso de $g$, recordemos que la división entre cero no está definida, entonces, $x\neq 0$. Por lo tanto, $D_{g}=\mathbb{R}-\left\{0 \right\}$.
b) Obtener las expresiones de las funciones $\left(\frac{f}{g}\right)(x)$ y $\bigl(g \circ f\bigr)(x)$, así como sus respectivos dominios.
Obtenemos la regla de correspondencia de $\left(\frac{f}{g}\right)(x)$ \begin{align*} \left(\frac{f}{g}\right)(x) &= \frac{f(x)}{g(x)} \\ &= \frac{\sqrt{x-5}}{\dfrac{x-1}{x}} \\ &= \sqrt{x-5}\,\cdot \frac{x}{x-1} \\ &= \frac{x\,\sqrt{x-5}}{x-1}. \end{align*} A continuación, determinamos el dominio. Para que $\sqrt{x-5}$ esté definida, se requiere $x - 5 \ge 0$, es decir, $x \ge 5$. Además, al encontrarse $g(x) = \tfrac{x-1}{x}$ en el denominador, se necesita $x \neq 0$ y $\tfrac{x-1}{x} \neq 0$, lo que equivale a $x \neq 1$. Sin embargo, el intervalo $x \ge 5$ no incluye a 0 ni a 1, por lo que al hacer la intersección de todas las condiciones obtenemos el dominio \begin{align*} D_{\frac{f}{g}}=[5, \infty). \end{align*} Ahora, al regla de correspondencia de la composición es \begin{align*} \bigl(g \circ f\bigr)(x) &= g\bigl(f(x)\bigr) = g\bigl(\sqrt{x-5}\bigr) = \frac{\sqrt{x-5} - 1}{\sqrt{x-5}}= 1-\frac{1}{\sqrt{x-5}}. \end{align*} Para determinar el dominio, para que $f(x) = \sqrt{x-5}$ esté definida, se requiere $x \ge 5$. Luego, para que la expresión $\frac{\sqrt{x-5} - 1}{\sqrt{x-5}}$ esté definida, se necesita $\sqrt{x-5} \neq 0$, lo cual equivale a $x > 5$. Por lo tanto, el dominio de $\bigl(g \circ f\bigr)(x)$ es $(5, \infty)$.
4. Considerar una caja con base rectangular y sin tapa.
El largo de la base es el doble del ancho y, a su vez, es el triple de la altura de la caja.
Determinar la expresión del área superficial de la caja en función del ancho de la base.
Consideramos una caja con base rectangular y sen tapa. Denotamos con $w$ el ancho de la base. Por hipótesis, el largo $L$ de la base es el doble del ancho, de modo que $L = 2w$, y a su vez el largo es el triple de la altura $h$, por lo que $h = \frac{L}{3} = \frac{2w}{3}$. El área superficial sen tapa se compone del área de la base más el área de las cuatro paredes. La base, de dimensiones $L \times w$, aporta un área $L w$. Las dos paredes que comparten el largo y la altura aportan un área total de $2 \cdot (L \cdot h)$, mientras que las dos paredes que comparten el ancho y la altura aportan $2 \cdot (w \cdot h)$. De este modo, denotando el área superficial por $S(w)$, tenemos \begin{align*} S(w) &= Lw + 2(L\,h) + 2(w\,h) \\ &= (2w)\,w + 2\Bigl((2w)\,\frac{2w}{3}\Bigr) + 2\Bigl(w\,\frac{2w}{3}\Bigr). \end{align*} Calculamos cada término y obtenemos \begin{align*} (2w)\,w &= 2w^2, \\ (2w)\,\frac{2w}{3} &= \frac{4w^2}{3}, \\ w\,\frac{2w}{3} &= \frac{2w^2}{3}. \end{align*} Por ello, \begin{align*} S(w) &= 2w^2 + 2\Bigl(\frac{4w^2}{3}\Bigr) + 2\Bigl(\frac{2w^2}{3}\Bigr) \\ &= 2w^2 + \frac{8w^2}{3} + \frac{4w^2}{3} = 2w^2 + \frac{12w^2}{3} = 2w^2 + 4w^2 = 6w^2. \end{align*} Así, el área superficial de la caja sen tapa en función de $w$ es \[ S(w) = 6w^2. \]
1. Calcular los siguientes límites:
a) $\displaystyle \lim_{x \to 0} \frac{x \,\mathrm{sen}(2x)}{6x^2}$
Podemos reescribir la fracción para aislar el cociente $\frac{\mathrm{sen}(2x)}{2x}$. Procedemos de la siguiente forma, todo dentro de un solo límite: \[ \lim_{x \to 0} \frac{x \,\mathrm{sen}(2x)}{6\,x^2} = \lim_{x \to 0} \Bigl[ \frac{1}{6} \cdot \underbrace{\,2\,}_{\text{factor constante}} \cdot \frac{\mathrm{sen}(2x)}{2x} \Bigr] = \lim_{x \to 0} \Bigl[ \frac{2}{6} \cdot \frac{\mathrm{sen}(2x)}{2x} \Bigr]. \] Cuando $x \to 0$, también $2x \to 0$, y se sabe que $\displaystyle \lim_{u \to 0} \frac{\mathrm{sen}(u)}{u} = 1$. Aplicando esto se obtiene \[ \lim_{x \to 0} \frac{\mathrm{sen}(2x)}{2x} = 1, \] de modo que \[ \lim_{x \to 0} \frac{x \,\mathrm{sen}(2x)}{6\,x^2} = \frac{2}{6} \cdot \lim_{x \to 0}\frac{\mathrm{sen}(2x)}{2x} = \frac{2}{6} \cdot 1 = \frac{1}{3}. \] Por lo tanto, el valor del límite es \[ \frac{1}{3}. \]
b) $\displaystyle \lim_{x \to 2} \frac{\sqrt{x^2 + 12} - 4}{x^2 - 2x}$
Buscamos el valor del límite \[ \lim_{x \to 2} \frac{\sqrt{x^{2}+12} - 4}{x^{2}-2x}. \] En primer lugar, al intentar sustituir $x=2$ directamente, se obtiene \[ \sqrt{2^2 + 12} - 4 = \sqrt{16} - 4 = 4 - 4 = 0, \] y \[ 2^2 - 2\cdot 2 = 4 - 4 = 0, \] de modo que la expresión adopta la forma indeterminada $\frac{0}{0}$. Para resolverla, racionalizamos el numerador multiplicando y dividiendo por el conjugado $\sqrt{x^2+12} + 4$: \[ \frac{\sqrt{x^{2}+12} - 4}{x^{2}-2x} \,\cdot\, \frac{\sqrt{x^{2}+12} + 4}{\sqrt{x^{2}+12} + 4} = \frac{(\sqrt{x^{2}+12} - 4)(\sqrt{x^{2}+12} + 4)}{(x^{2} - 2x)\,\bigl(\sqrt{x^{2}+12} + 4\bigr)}. \] El producto del numerador con su conjugado es \[ (\sqrt{x^{2}+12})^2 - 4^2 = (x^{2} + 12) - 16 = x^2 - 4. \] Por tanto, \[ \frac{\sqrt{x^{2}+12} - 4}{x^{2}-2x} = \frac{x^2 - 4}{(x^2 - 2x)\,\bigl(\sqrt{x^{2}+12} + 4\bigr)}. \] A continuación, factorizamos el numerador y parte del denominador: \[ x^2 - 4 = (x-2)(x+2), \qquad x^2 - 2x = x(x-2). \] De esta manera, la fracción se simplifica: \[ \frac{x^2 - 4}{(x^2 - 2x)\,\bigl(\sqrt{x^{2}+12} + 4\bigr)} = \frac{(x-2)(x+2)}{\,x(x-2)\,\bigl(\sqrt{x^{2}+12} + 4\bigr)} = \frac{x+2}{\,x\,\bigl(\sqrt{x^{2}+12} + 4\bigr)} \quad (\text{si } x \neq 2, \, x \neq 0). \] Ahora sí podemos calcular el límite cuando $x \to 2$: \[ \lim_{x \to 2} \frac{x+2}{\,x\,\bigl(\sqrt{x^{2}+12} + 4\bigr)} = \frac{\,2 + 2\,}{\,2\,\bigl(\sqrt{2^{2} + 12} + 4\bigr)} = \frac{4}{\,2\,(\sqrt{16} + 4)} = \frac{4}{\,2\,(4+4)} = \frac{4}{2\cdot 8} = \frac{4}{16} = \frac{1}{4}. \] Por lo tanto, \[ \lim_{x \to 2} \frac{\sqrt{x^{2}+12} - 4}{x^{2}-2x} = \frac{1}{4}. \]
2. Dada la función $f(x) = \mathrm{sen}(x)$:
a) Realizar el bosquejo de la gráfica de $h(x) = -2f(2x) + 3$, en el intervalo $[0, 2\pi]$.
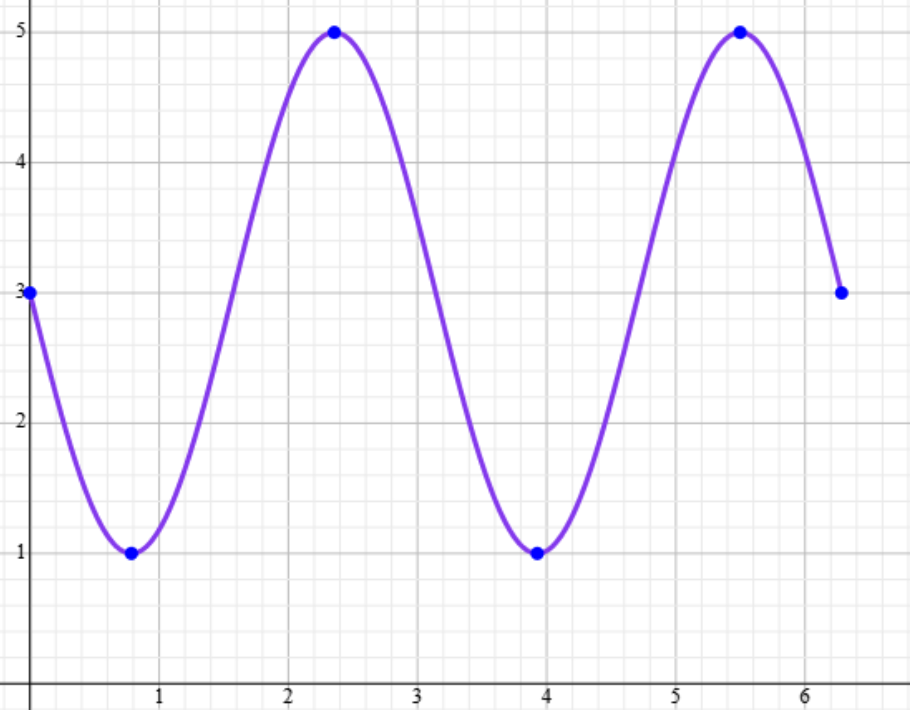
b) Obtener la amplitud, frecuencia y el período de $h(x)$.
La forma $\mathrm{sen}(2x)$ indica que la frecuencia de la onda es 2, pues $\mathrm{sen}(Bx)$ tiene frecuencia $B$. También podemos ver que el período de $\mathrm{sen}(2x)$ es $\pi$, dado que el período de $\mathrm{sen}(x)$ es $2\pi$ y se divide entre 2 al tener $\mathrm{sen}(2x)$. Al haberse multiplicado la función por $-2$, la amplitud se convierte en 2. En resumen: \[ \text{Amplitud} = 2,\quad \text{Frecuencia} = 2,\quad \text{Período} = \frac{2\pi}{2} = \pi. \]
c) Describir los desplazamientos, las reflexiones, elongaciones y contracciones para obtener la gráfica de la función $h(x)$.
$f(x)=\mathrm{sen}{x}$
$g(x)=f(2x)$ compresión a lo largo del eje $x$ (dividir entre 2 a las $x$).
$r(x)=-g(x)$ reflexión respecto al eje $x$ (multiplicar por $-1$ a las $y$).
$l(x)=2r(x)$ elongación a lo largo del eje $y$ (multiplicar por 2 a las $y$).
$h(x)=l(x)+3$ desplazamiento o traslación sobre el eje $y$ hacia arriba (sumar 3 a a las $y$).
De este modo, la gráfica final se obtiene aplicando sucesivamente esas transformaciones a la función $\mathrm{sen}(x)$.
3. Para la función por partes $f (x)$, calcular:
\[\lim_{x \to -3^+} f(x),\] donde
\[f(x) =
\begin{cases}
\sqrt{x - 3}, & \text{si } x \le -3,\\[6pt]
\dfrac{x^2 + 3x}{x + 3}, & \text{si } x > -3.
\end{cases}
\]
Queremos calcular \[ \lim_{x \to -3^+} f(x). \] Dado que el límite se toma cuando $x$ tiende a $-3$ \emph{desde la derecha}, la definición pertinente de $f(x)$ es la correspondiente a $x > -3$: \[ f(x) = \frac{x^2 + 3x}{x + 3}. \] Para simplificar este cociente, factorizamos el numerador: \[ x^2 + 3x = x(x + 3). \] Así, mientras $x \neq -3$, podemos cancelar $x+3$ en numerador y denominador: \[ \frac{x^2 + 3x}{x + 3} = \frac{x(x+3)}{x+3} = x. \] Por lo tanto, cerca de $-3$ (pero con $x > -3$), la función se comporta como $f(x) = x$. Entonces \[ \lim_{x \to -3^+} \frac{x^2 + 3x}{x + 3} = \lim_{x \to -3^+} x = -3. \] De este modo, concluimos que \[ \lim_{x \to -3^+} f(x) = -3. \]
1. Calcular el siguiente límite:
\[\lim_{x \to -\infty} \frac{\sqrt{9x^2 - 2x}}{x}.\]
Tenemos que \begin{align*} \lim_{x \to -\infty}\frac{\sqrt{9x^{2}-2x}}{x}&=\lim_{x \to -\infty}\frac{\sqrt{x^{2}\left(9-\frac{2}{x} \right)}}{x}=\lim_{x \to -\infty} \frac{|x|\sqrt{9-\frac{2}{x}}}{x}=\lim_{x \to -\infty} \frac{-x\sqrt{9-\frac{2}{x}}}{x}\\ &=\lim_{x \to -\infty} -\sqrt{9-\frac{2}{x}}=-3. \end{align*}
2. Sea la función:
\[g(x) = \frac{x^2 - x - 6}{x^2 - 5x + 6}.\]
a) Determinar el dominio y las raíces.
Dominio. Factorizamos numerador y denominador: \[ x^2 - x - 6 \;=\; (x-3)(x+2), \quad\quad x^2 - 5x + 6 \;=\; (x-3)(x-2). \] Por tanto, \[ g(x) \;=\; \frac{(x-3)(x+2)}{\,(x-3)(x-2)\,}. \] La única restricción del dominio proviene de los ceros del denominador. Vemos que \[ x-3 = 0 \quad\Longrightarrow\quad x=3, \quad\quad x-2 = 0 \quad\Longrightarrow\quad x=2. \] Por lo tanto, \[ D_{g} \;=\; \mathbb{R}-\{\,2,\,3\}. \] Raíces. Para hallar las raíces de $g$ basta con resolver $g(x) = 0$, esto es, que su numerador sea cero (y que el denominador no se anule simultáneamente): \[ x^2 - x - 6 = (x-3)(x+2)=0 \;\Longrightarrow\; x=3 \,\text{ o }\, x=-2. \] Sin embargo, $x=3$ no pertenece al dominio (pues anula tanto numerador como denominador). Por lo tanto, la única raíz de $g$ (dentro de su dominio) es \[ x=-2. \]
b) Obtener las ecuaciones de las asíntotas horizontales y verticales.
Asíntota vertical. Al factorizar, \[ g(x) \;=\; \frac{(x-3)(x+2)}{(x-3)(x-2)} \;=\; \frac{x+2}{x-2} \quad\text{para } x \neq 3. \] Se aprecia que $x=2$ \emph{no} se simplifica, de modo que en $x=2$ la función no está definida y es donde se presenta una asíntota vertical. En cambio, la supuesta singularidad en $x=3$ se anula arriba y abajo, originando un \emph{agujero} (discontinuidad removible), no una asíntota. Por ende, la única asíntota vertical es \[ x=2. \] Asíntota horizontal. Para $x$ grande en valor absoluto, la función \[ g(x) =\frac{x^2 - x - 6}{x^2 - 5x + 6} \] se comporta como $\frac{x^2}{x^2} \approx 1$. Más rigurosamente, \[ \lim_{x\to\pm\infty} \frac{x+2}{x-2} = \lim_{x\to\pm\infty} \frac{x(1+\tfrac{2}{x})}{\,x(1-\tfrac{2}{x})\,} = \frac{1+0}{\,1-0\,} = 1. \] Así, la única asíntota horizontal es \[ y=1. \]
c) Elaborar un bosquejo de su gráfica.
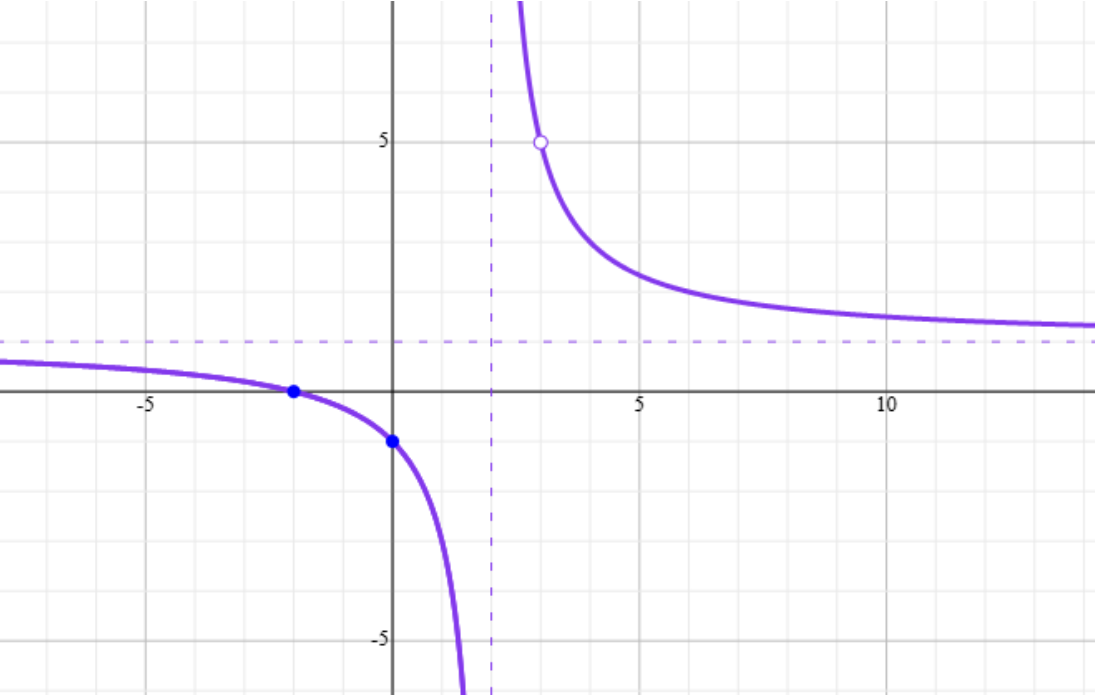
d) Determinar las discontinuidades y su clasificación, así como los intervalos de continuidad.
Discontinuidades.
3. Obtener los valores de las constantes a y b para que la siguiente función sea continua en su dominio
\[f(x) =
\begin{cases}
\displaystyle \frac{x^2 - 4}{x + 2}, & \text{si } x < -2,\\[6pt]
ax + 3, & \text{si } -2 \le x \le 2,\\[6pt]
x^2 - b, & \text{si } x > 2.
\end{cases}
\]
Queremos determinar $a$ y $b$ para que $f(x)$ sea continua en todo su dominio, en particular en los puntos de transición $x=-2$ y $x=2$. Continuidad en $x = -2$. Para $x < -2$, el valor de la función es \[ \frac{x^2 - 4}{x + 2}. \] Podemos factorizar el numerador: \[ x^2 - 4 = (x-2)(x+2). \] Mientras $x \neq -2$, se simplifica \[ \frac{x^2 - 4}{x + 2} = \frac{(x-2)(x+2)}{x+2} = x - 2. \] Por tanto, \[ \lim_{x \to -2^-} f(x) = \lim_{x \to -2^-} \bigl(x - 2\bigr) = -2 - 2 = -4. \] A su vez, para que $f$ sea continua en $x = -2$, debemos tener \[ f(-2) = \lim_{x \to -2^-} f(x). \] Pero cuando $-2 \le x \le 2$, la definición de $f$ es $f(x) = ax + 3$. Entonces \[ f(-2) = a(-2) + 3 = -2a + 3. \] La condición de continuidad da \[ -2a + 3 = -4 \quad\Longrightarrow\quad -2a = -7 \quad\Longrightarrow\quad a = \frac{7}{2}. \] Continuidad en $x = 2$. Para $-2 \le x \le 2$, ahora sabemos que $f(x) = \tfrac{7}{2}\,x + 3$. En particular, \[ f(2) = \frac{7}{2}\cdot 2 + 3 = 7 + 3 = 10. \] Para $x > 2$, la definición de $f$ es $f(x) = x^2 - b$. Por tanto, si $f$ es continua en $x=2$, se requiere que \[ \lim_{x \to 2^+} \bigl(x^2 - b\bigr) = f(2). \] Como $x^2 - b$ es continua en sí misma, basta evaluar en $x=2$: \[ 2^2 - b = 4 - b. \] La continuidad exige \[ 4 - b = 10 \quad\Longrightarrow\quad -b = 6 \quad\Longrightarrow\quad b = -6. \] Por lo tanto, los valores que hacen continua la función en su dominio son \[ \boxed{a = \frac{7}{2}, \quad b = -6.} \]
4. Encontrar un intervalo de longitud $\displaystyle \frac{\pi}{4}$ o menor que contenga una solución de la ecuación:
\[\mathrm{sen}(x) - x + 2 = 0.\]
Justificar la respuesta.
Buscamos un intervalo de longitud no mayor que $\tfrac{\pi}{4}$ que contenga una solución de la ecuación \[ \mathrm{sen}(x) \;-\; x \;+\; 2 \;=\; 0. \] Definamos la función \[ f(x) \;=\; \mathrm{sen}(x) \;-\; x \;+\; 2. \] Observamos que un cero de $f(x)$ equivale a una solución de la ecuación dada. En primer lugar, evaluamos $f$ en algunos valores (aproximados) para acotar un cambio de signo. Probemos con: \[ f(2.5) = \mathrm{sen}(2.5) \;-\; 2.5 \;+\; 2, \quad f(2.6) = \mathrm{sen}(2.6) \;-\; 2.6 \;+\; 2. \] Numéricamente, \[ \mathrm{sen}(2.5) \approx 0.59847, \quad\;\; \mathrm{sen}(2.6) \approx 0.51550. \] Por tanto: \[ f(2.5) \approx 0.59847 \;-\; 2.5 \;+\; 2 = 0.59847 - 0.5 = 0.09847 \quad (\text{positivo}), \] \[ f(2.6) \approx 0.51550 \;-\; 2.6 \;+\; 2 = 0.51550 - 0.6 = -0.08450 \quad (\text{negativo}). \] Vemos que $f(2.5)$ y $f(2.6)$ tienen signos opuestos, por lo que el Teorema del Valor Intermedio garantiza la existencia de al menos un número $c\in(2.5, 2.6)$ tal que $f(c)=0$. Nótese que $\,2.6 - 2.5 = 0.1$, y claramente \[ 0.1 \;<\; \frac{\pi}{4} \,\approx\, 0.785. \] De modo que el intervalo $[2.5, 2.6]$ (de longitud 0.1) contiene una solución de la ecuación $\mathrm{sen}(x) - x + 2 = 0$, satisfaciendo el requisito de que la longitud sea menor o igual que $\tfrac{\pi}{4}$.